
【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=135°,CD=6,AB=2,则四边形ABCD的面积为___________

【答案】16
【解析】
延长AB和DC,两线交于O,求出OB=![]() BC,OD=
BC,OD=![]() OA,OA=AD,BC=OC,设BC=OC=x,则BO=
OA,OA=AD,BC=OC,设BC=OC=x,则BO=![]() x,解直角三角形得出方程,求出x,再分别求出△AOD和△BOC的面积即可.
x,解直角三角形得出方程,求出x,再分别求出△AOD和△BOC的面积即可.
延长AB和DC,两线交于O,
∵∠C=90°,∠ABC=135°,
∴∠OBC=45°,∠BCO=90°,
∴∠O=45°,
∵∠A=90°,
∴∠D=45°,
则OB=![]() BC,OD=
BC,OD=![]() OA,OA=AD,BC=OC,
OA,OA=AD,BC=OC,
设BC=OC=x,则BO=![]() x,
x,
∵CD=6,AB=2,
∴6+x=![]() (
(![]() x+2),
x+2),
解得:x=6-2![]() ,
,
∴OB=6![]() -4,BC=OC=6-2
-4,BC=OC=6-2![]() ,OA=AD=2+6
,OA=AD=2+6![]() -4=6
-4=6![]() -2,
-2,
∴S四边形ABCD=S△OAD-S△OBC
=![]() OAAD-
OAAD-![]() BCOC
BCOC
=![]()
=16,
故答案为:16.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】某校在甲、乙两名同学中选拔一人参加襄阳广播电台举办“国学风,少年颂”襄阳首届少年儿童经典诵读大赛.在相同的测试条件下,两人3次测试成绩(单位:分)如下:甲:79,86,82;乙:88,79,90.从甲、乙两人3次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部分为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额的数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
该商场服装营业员的人数为 ,图①中m的值为 ;
求统计的这组销售额数据的平均数、众数和中位数.

查看答案和解析>>
科目:初中数学 来源: 题型:
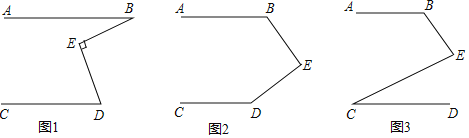
【题目】直线![]() 为直线AB、CD之间的一点.
为直线AB、CD之间的一点.
![]() 如图1,若
如图1,若![]() ,则
,则![]() ______ ;
______ ;
![]() 如图2,若
如图2,若![]() ,则
,则![]() ______ ;
______ ;
![]() 如图3,若
如图3,若![]() ,则
,则![]() 、
、![]() 与
与![]() 之间有什么等量关系?请猜想证明.
之间有什么等量关系?请猜想证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P1、P2是反比例函数y= ![]() (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点. 
(1)求反比例函数的解析式.
(2)①求P2的坐标. ②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y= ![]() 的函数值.
的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
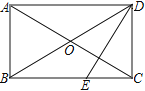
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
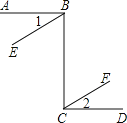
【题目】如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程
![]() 题设
题设![]() 已知
已知![]() ;______
;______
结论![]() 求证
求证![]() :______
:______
理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣ ![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.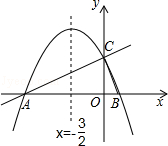
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com