
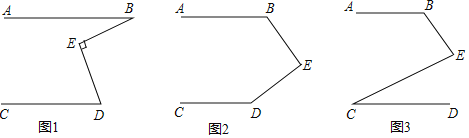
【题目】直线![]() 为直线AB、CD之间的一点.
为直线AB、CD之间的一点.
![]() 如图1,若
如图1,若![]() ,则
,则![]() ______ ;
______ ;
![]() 如图2,若
如图2,若![]() ,则
,则![]() ______ ;
______ ;
![]() 如图3,若
如图3,若![]() ,则
,则![]() 、
、![]() 与
与![]() 之间有什么等量关系?请猜想证明.
之间有什么等量关系?请猜想证明.
【答案】![]() ;
;![]()
【解析】
(1)过E作EF∥AB,根据两直线平行,内错角相等进行计算;
(2)过E作EF∥AB,根据两直线平行,同旁内角互补进行计算;
(3)过点E作EF∥AB,根据两直线平行,内错角相等,以及两直线平行,同旁内角互补进行计算.
(1)过E作EF∥AB,
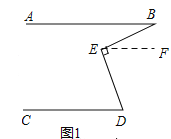
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
故答案为:75°;
(2)过E作EF∥AB,
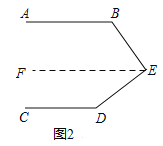
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°-α-β,
(3)猜想:∠BED=180°-α+β.
证明:过点E作EF∥AB,
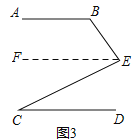
则∠BEF=180°-∠B=180°-α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°-α+β.


科目:初中数学 来源: 题型:
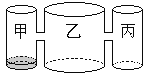
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )

A. 115° B. 105° C. 95° D. 85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
请结合图表完成下列各题:
(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率. 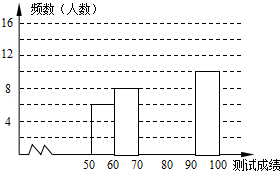
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图. 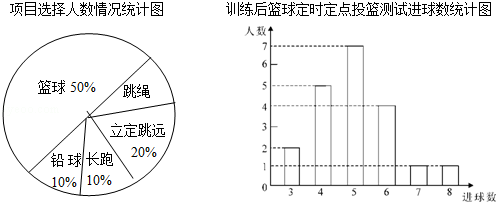
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为度,该班共有学生人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+4![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() ,其中正确的结论是( )
,其中正确的结论是( )

A. ①②③⑤ B. ①②③④ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com