
【题目】已知a≥2,m2﹣2am+2=0,n2﹣2an+2=0,则(m﹣1)2+(n﹣1)2的最小值是( )
A.6
B.3
C.﹣3
D.0
【答案】A
【解析】解:∵m2﹣2am+2=0,n2﹣2an+2=0,
∴m,n是关于x的方程x2﹣2ax+2=0的两个根,
∴m+n=2a,mn=2,
∴(m﹣1)2+(n﹣1)2=m2﹣2m+1+n2﹣2n+1=(m+n)2﹣2mn﹣2(m+n)+2=4a2﹣4﹣4a+2=4(a﹣ ![]() )2﹣3,
)2﹣3,
∵a≥2,
∴当a=2时,(m﹣1)2+(n﹣1)2有最小值,
∴(m﹣1)2+(n﹣1)2的最小值=4(a﹣ ![]() )2+3=4(2﹣
)2+3=4(2﹣ ![]() )2﹣3=6,
)2﹣3=6,
故选A.
【考点精析】关于本题考查的根与系数的关系和二次函数的最值,需要了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.某种彩票中奖的概率是 ![]() ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B.了解一批电视机的使用寿命适合用抽样调查
C.若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D.在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动.小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查.她在300户家庭中随机调查了50户家庭5月份的用水量,结果如图所示.把图中每组用水量的值用该组的中间值(如0~6的中间值为3)来代替,估计该小区5月份的用水量.
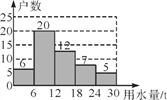
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠A=90°,AB=AC=![]() +1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
+1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0). 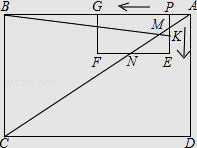
(1)当t=1时,KE= , EN=;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() , 求BC和BF的长.
, 求BC和BF的长.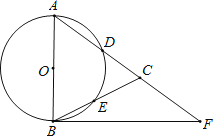
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从图![]() 所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
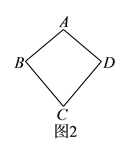
具体定义如下:如图![]() ,在四边形
,在四边形![]() 中,
中, ![]() ,
, ![]() ,我们把这种两组邻边分别相等的四边形叫做“筝形”.
,我们把这种两组邻边分别相等的四边形叫做“筝形”.

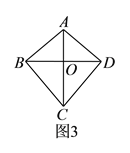
(![]() )结合图
)结合图![]() ,通过观察、测量、折纸,可以猜想“筝形”具有诸如“
,通过观察、测量、折纸,可以猜想“筝形”具有诸如“![]() 平分
平分![]() 和
和![]() ”这样的性质,请结合图形,再写出两条“筝形”的性质.
”这样的性质,请结合图形,再写出两条“筝形”的性质.
①____________________________.
②____________________________.
(![]() )从你写出的两条性质中,任选一条“筝形”的性质给出证明.
)从你写出的两条性质中,任选一条“筝形”的性质给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1、x2 , 且x1≠x2 , 有下列结论:①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是( )
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com