
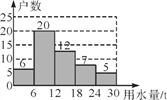
����Ŀ��Ϊ��߾���Ľ�ˮ��ʶ������С����չ���������ˮ��������������ˮ��ȫ��Ϊ����Ľ�ˮ�������СӨͬѧ��������С���������������С��300����ͥ��ˮ��������˳������飮����300����ͥ�����������50����ͥ5�·ݵ���ˮ���������ͼ��ʾ����ͼ��ÿ����ˮ����ֵ�ø�����м�ֵ(��0��6���м�ֵΪ3)�����棬���Ƹ�С��5�·ݵ���ˮ����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �Ƿ���������
�Ƿ���������![]() ͼ����һ�㣬��
ͼ����һ�㣬��![]() ���ڵ�
���ڵ�![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ����Ϊ
����Ϊ![]() ��
��

��![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��![]() ����ֱ��
����ֱ��![]() ������
������![]() ������һ֧˫�����ڵ�
������һ֧˫�����ڵ�![]() ����
����![]() �������
�������
��![]() ��ָ��
��ָ��![]() ȡ��ֵʱ��һ�κ�����ֵ���ڷ�����������ֵ��ֱ��д�������
ȡ��ֵʱ��һ�κ�����ֵ���ڷ�����������ֵ��ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��֤ѧ�����㹻��˯�ߣ���ЭίԱ�ڽ��������������һ���鰸�������Ƴ���Сѧ���糿�Ͽ�ʱ�䡱������鰸�����õ������˴������֧�֣����ݱ����н�ί��Ҫ��ѧ��Сǿ����ѧУ��ѧ����Уʱ���Ƴٰ�Сʱ��Сǿԭ��7��Ӽҳ�����������������7��20�ֵ�У������Сǿ���ɸ�ĸ����������ѧ��7��45�ֳ�����7��50�־͵�ѧУ�ˣ���֪Сǿ���Լҳ��ȳ˹�����ƽ��ÿСʱ��36ǧ�ף����Сǿ�ҵ�ѧУ��·���Ƕ���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������л�����ѧ���ݽ������У���λ��ί�ֱ���ס�����λѡ�ֵ��������£��ף�8��7��9��8��8���ң�7��9��6��9��9��������˵���д������( )
A. �ס��ҵ÷ֵ�ƽ��������8 B. �÷ֵ�������8���ҵ÷ֵ�������9
C. �÷ֵ���λ����9���ҵ÷ֵ���λ����6 D. �÷ֵķ�����ҵ÷ֵķ���С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=ax2+bx+3��a��0����x�ᡢy��ֱ��ڵ�A����1��0����B��3��0������C���㣮
��1�����������ߵĽ���ʽ��
��2����D��2��m���ڵ�һ�����������ϣ�����BC��BD�����ʣ��ڶԳ����������������Ƿ����һ��P�������PBC=��DBC��������ڣ��������P������ꣻ��������ڣ���˵�����ɣ�
��3����ͼ2���ڣ�2���������£�����BOC��x����������ÿ��1����λ���ȵ��ٶ�����ƽ�ƣ���ƽ�ƺ��������Ϊ��B��O��C�䣮��ƽ�ƹ����У���B��O��C�����BCD�ص��������ΪS����ƽ�Ƶ�ʱ��Ϊt�룬����S��t֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ������![]() ����˼����С������������̽����
����˼����С������������̽����
��![]() ����a��b��m��n������
����a��b��m��n������![]() ������
������![]() ��
��
![]() ����С�����ҵ���һ�ְ�����
����С�����ҵ���һ�ְ�����![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺
![]() ��a��b��m��n��Ϊ������ʱ����
��a��b��m��n��Ϊ������ʱ����![]() ���ú�m��n��ʽ�ӷֱ��ʾa��b���ã�
���ú�m��n��ʽ�ӷֱ��ʾa��b���ã� ![]() ______��
______�� ![]() ______��
______��
![]() ������̽���Ľ��ۣ�����һ��������a��b��m��n��գ�
������̽���Ľ��ۣ�����һ��������a��b��m��n��գ�
______![]() _____
_____![]() ______
______![]()
______![]() ��
��
![]() ��
��![]() ��a��m��n��Ϊ����������a��ֵ��
��a��m��n��Ϊ����������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
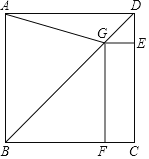
����Ŀ����ͼ����������ABCD�У���G�ڶԽ���BD��![]() �����
�����![]() �غ�
�غ�![]() �ڵ�
�ڵ�![]() �ڵ�F������AG��
�ڵ�F������AG��
![]() д���߶�
д���߶�![]() ����֮���������ϵ����˵�����ɣ�
����֮���������ϵ����˵�����ɣ�
![]() ��������ABCD�ı߳�Ϊ
��������ABCD�ı߳�Ϊ![]() �����߶�BG�ij���
�����߶�BG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��2��m2��2am+2=0��n2��2an+2=0����m��1��2+��n��1��2����Сֵ�ǣ�������
A.6
B.3
C.��3
D.0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��1��0����B��0��-1����C��-1��2����D��2��-1����E��4��2������㣬������y=a��x-1��2+k��a��0���������е������㣮
��1����֤��C��E���㲻����ͬʱ��������y=a��x-1��2+k��a��0���ϣ�
��2����A��������y=a��x-1��2+k��a��0������Ϊʲô��
��3����a��k��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com