
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:不详 题型:单选题
| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
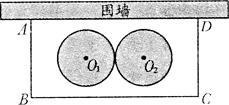
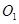 和
和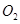 ,且
,且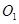 到AB、BC、AD的距离与
到AB、BC、AD的距离与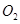 到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,清说明理由.
到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,清说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.10cm | B.30cm | C.40cm | D.300cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
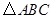 中,
中,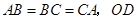 、
、 为
为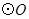 的半径,
的半径,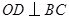 于
于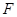 ,
,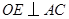 于点
于点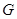 ,求证:
,求证:
 阴影部分四边形
阴影部分四边形 的面积是
的面积是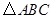 的面积的
的面积的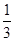 .
.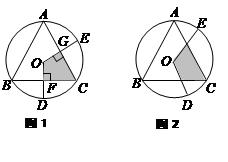
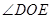 保持
保持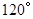 角度不变,求证:当
角度不变,求证:当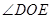 绕着
绕着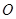 点旋转时,由两条半径
点旋转时,由两条半径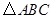 的两条边围成的图形(图中阴影部分)面积始终是
的两条边围成的图形(图中阴影部分)面积始终是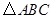 的面积的
的面积的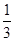 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com