
 的最值.
的最值. 化为关于x的二次方程(1-y)x2+2(a-by)x+(1-y)=0,
化为关于x的二次方程(1-y)x2+2(a-by)x+(1-y)=0,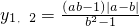 ,可得
,可得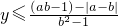 或
或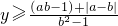 ,
,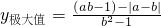 ,
,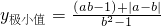 ;
;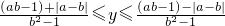 ,
,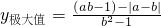 ,
,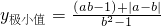 ;
;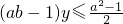 ,
,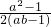 ,∴
,∴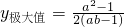 ;
;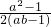 ,∴
,∴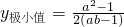 .
. 化为关于x的一元二次方程:(1-y)x2+2(a-by)x+(1-y)=0,从而得出△≥0,将本题视为在△≥0的情况下求y的最值,然后讨论b的范围,在b不同范围内求出y的最值.
化为关于x的一元二次方程:(1-y)x2+2(a-by)x+(1-y)=0,从而得出△≥0,将本题视为在△≥0的情况下求y的最值,然后讨论b的范围,在b不同范围内求出y的最值.

科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第2期 总第158期 沪科版 题型:044
在实际问题中求函数的最值时,要将函数关系式写成什么形式?顶点的纵坐标一定是函数的最值吗?如果顶点的纵坐标不是函数的最值,应如何求函数的最值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com