
【题目】在□ABCD中,AD=BD,BE是AD边上的高,∠EBD=28°,则∠A的度数为_______.
【答案】59°或31°
【解析】
分析题意,首先根据已知作出图,由于△ABD的形状不确定,故需分类讨论:
当E点在线段AD上时,首先求出∠ADB的度数,再利用三角形内角和定理以及等腰三角形的性质,得出∠A的度数;
当E点在AD的延长线上时,结合已知可先求出∠BDE的度数,然后根据等腰三角形的性质以及三角形外角的性质进行求解即可
情况一:当E点在线段AD上时,如图所示:
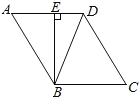
∵BE是AD边上的高,∠EBD=28°,
∴∠ADB=90°-28°=62°.
∵AD=BD,
∴∠A=∠ABD=(180°-62°)÷2=59°.
情况二:当E点在AD的延长线上时,如图所示:
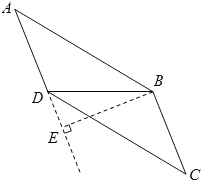
∵BE是AD边上的高,∠EBD=28°,
∴∠BDE=62°,
∵AD=BD,
∴∠A=∠ABD=![]() ∠BDE=
∠BDE=![]() ×62°=31°.
×62°=31°.
综上可知,∠A的度数为59° 或31°.
故答案为:59° 或31°.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )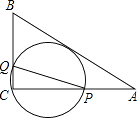
A.5
B.4 ![]()
C.4.75
D.4.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
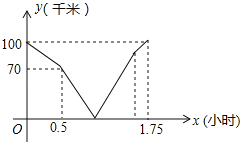
A. 乙先出发的时间为0.5小时 B. 甲的速度是80千米/小时
C. 甲出发0.5小时后两车相遇 D. 甲到B地比乙到A地早![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
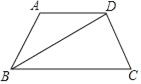
【题目】如图,四边形ABCD中,AD∥BC,∠A=120°,BD平分∠ABC.
(1)若BD⊥CD,求∠C的度数;
(2)射线AP从AB位置开始,以每秒10°的速度绕点A逆时针旋转,6秒后AP与BD有何种位置关系?并说明理由.
(3)在(2)的条件下,AP旋转一圈回到AB处时停止运动,若射线AP与直线BD相交所成的角中较小的角为x°,当10<x<20,则旋转时间t(单位:秒)的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潜山市某村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )

A. 1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少
B. 1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平
C. 1月至3月每月生产总量逐月增加,4、5两月均停止生产
D. 1月至3月每月生产总量不变,4、5两月均停止生产
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0)、B(4,1)两点,且与y轴交于点C.
(1)求抛物线的解析式;
(2)如图(1),设抛物线与x轴的另一个交点为D,在抛物线的对称轴上找一点H,使△CDH的周长最小,求出H点的坐标并求出最小周长值.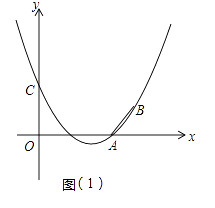
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣ ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,SABCD=24,则k1= . 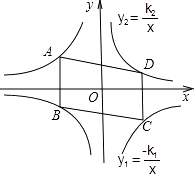
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求三次传球后,球回到甲脚下的概率;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com