解:(1)从图象可知,当6≤t≤8时,△ABP面积不变
即6≤t≤8时,点P从点C运动到点D,且这时速度为每秒2个单位
∴CD=2(8-6)=4
∴AB=CD=4
当t=6时(点P运动到点C),S
△ABP=16
∴
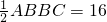
∴
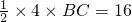
∴BC=8
∴长方形的长为8,宽为4.
(2)当t=a时,S
△ABP=8=
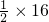
即点P此时在BC的中点处
∴PC=

=
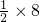
=4
∴2(6-a)=4
∴a=4
∵BP=PC=4
∴m=
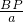
=
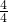
=1
当t=b时,S
△ABP=
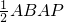
=4
∴
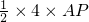
=4,AP=2
∴b=13-2=11;
(3)当8≤t≤11时,S关于t的函数图象是过点(8,16),(11,4)的一条直线
可设S=kt+b
∴
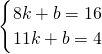
∴
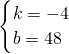
∴S=-4t+48(8≤t≤11)
同理可求当11≤t≤13时S关于t的函数解析式
S=-2t+26(11≤t≤13)
分析:(1)由图象可知,CD的长度,当t=6时,S
△ABP=16,求出BC的长;
(2)当t=a时,S
△ABP=8,则点P此时在BC的中点处,从而得出a和m的值,当t=b时,S
△ABP=4,从而求得b的值;
(3)设S=kt+b,根据函数图象是过点(8,16),(11,4),代入即可认得出答案.
点评:本题是一次函数的综合题,考查了学生观察图象的能力,用待定系数法求一次函数的解析式,是一道中考压轴题.


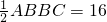
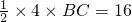
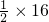
 =
=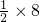 =4
=4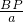 =
=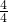 =1
=1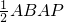 =4
=4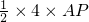 =4,AP=2
=4,AP=2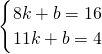 ∴
∴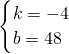


 如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)
如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)