Question

已知，在矩形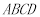中，连接对角线，将绕点顺时针旋转得到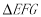，并将它沿直线向左平移，直线与交于点，连接，．

（1）如图①，当，点平移到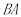线段上时，线段有怎样的数量关系和位置关系？直接写出你的猜想；

（2）如图②，当，点平移到线段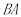的延长线上时，（1）中的结论是否成立，请说明理由；

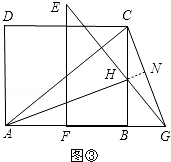
（3）如图③，当时，对矩形进行如已知同样的变换操作，线段有怎样的数量关系和位置关系？直接写出你的猜想．

图① 图② 图③

 

Answer 1

（1）AH=CG,AH⊥CG；

AH=CG,AH⊥CG，理由见解析；

AH=nCG，AH⊥CG．

【解析】

试题分析：（1）延长AH与CG交于点T，如图①，易证BH=BG，从而可证到△ABH≌△CBG，则有AH=CG，∠HAB=∠GCB，从而可证到∠HAB+∠AGC=90°，进而可证到AH⊥CG．

（2）延长CG与AH交于点Q，如图②，仿照（1）中的证明方法就可解决问题．

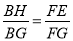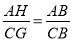（3）延长AH与CG交于点N，如图③，易证BH∥EF，可得△GBH∽△GFE，则有，也就有，从而可证到△ABH∽△CBG，则有=n，∠HAB=∠GCB，进而可证到AH=nCG，AH⊥CG．

试题解析：（1）AH=CG,AH⊥CG．

延长AH与CG交于点T，如图①，

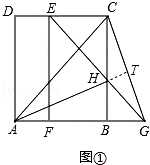
由旋转和平移的性质可得：EF=AB，FG=BC，∠EFG=∠ABC．

∵四边形ABCD是矩形，AB=BC，

∴EF=GF，∠EFG=∠ABC=90°．

∴∠CBG=90°，∠EGF=45°．

∴∠BHG=90°﹣45°=45°=∠EGF．

∴BH=BG．

在△ABH和△CBG中，

，

∴△ABH≌△CBG（SAS）．

∴AH=CG，∠HAB=∠GCB．

∴∠HAB+∠AGC=∠GCB+∠AGC=90°．

∴∠ATC=90°．

∴AH⊥CG．

（2）成立．理由如下：

延长CG与AH交于点Q，如图②，

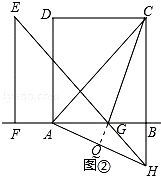
由旋转和平移的性质可得：EF=AB，FG=BC，∠EFG=∠ABC．

∵四边形ABCD是矩形，AB=BC，

∴EF=GF，∠EFG=∠ABC=90°．

∴∠ABH=90°，∠EGF=45°．

∴∠BGH=∠EGF=45°．

∴∠BHG=90°﹣45°=45°=∠BGH．

∴BH=BG．

在△ABH和△CBG中，

，

∴△ABH≌△CBG（SAS）．

∴AH=CG，∠HAB=∠GCB．

∴∠GCB+∠CHA=∠HAB+∠CHA=90°．

∴∠CQA=90°．

∴CG⊥AH．

AH=nCG，AH⊥CG

理由如下：

延长AH与CG交于点N，如图③，

由旋转和平移的性质可得：EF=AB，FG=BC，∠EFG=∠ABC．

∵四边形ABCD是矩形，AB=nBC，

∴EF=nGF，∠EFG=∠ABC=90°．

∴∠EFG+∠ABC=180°．

∴BH∥EF．

∴△GBH∽△GFE．

∴．

∵，

∴．

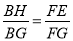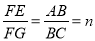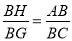∵∠ABH=∠CBG，

∴△ABH∽△CBG．

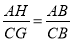∴=n，∠HAB=∠GCB．

∴AH=nCG，∠HAB+∠AGC=∠GCB+∠AGC=90°．

∴∠ANC=90°．

∴AH⊥CG．

考点：1、旋转的性质；2、矩形的性质3、全等三角形的判定与性质4、相似三角形的判定与性质．