
【题目】平面直角坐标系中,直线l1:y=﹣ ![]() x+3与x轴交于点A,与y轴交于点B,直线l2:y=kx+2k与x轴交于点C,与直线l1交于点P.
x+3与x轴交于点A,与y轴交于点B,直线l2:y=kx+2k与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
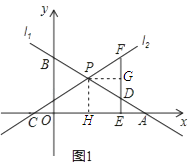
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
【答案】
(1)解:当k=1时,直线l2为y=x+2.
解方程组 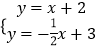 ,
,
解得 ![]() ,
,
∴P( ![]() ,
, ![]() );
);
(2)解:当y=0时,kx+2k=0,
∵k≠0,
∴x=﹣2,
∴C(﹣2,0)则OC=2,
当y=0时,﹣ ![]() x+3=0,
x+3=0,
∴x=6,
∴A(6,0),OA=6,
过点P作PG⊥DF于点G,
在△PDG和△ADE中,
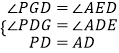 ,
,
∴△PDG≌△ADE,
得DE=DG= ![]() DF,
DF,
∴PD=PF,
∴∠PFD=∠PDF
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°
∴∠PCA=∠PAC,
∴PC=PA
过点P作PH⊥CA于点H,
∴CH= ![]() CA=4,
CA=4,
∴OH=2,
当x=2时,y=﹣ ![]() ×2+3=2代入y=kx+2k,得k=
×2+3=2代入y=kx+2k,得k= ![]()
(3)解:直角△PQR和直角△PMC中,
![]() ,
,
∴Rt△PMC≌Rt△PQR,
∴CM=RQ,
∴NR=NC,
设NR=NC=a,则R(﹣a﹣2,a),
代入y=﹣ ![]() x+3,
x+3,
得﹣ ![]() (﹣a﹣2)+3=a,解得a=8,
(﹣a﹣2)+3=a,解得a=8,
设P(m,n),则 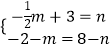 ,
,
解得 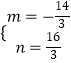 ,
,
∴P(﹣ ![]() ,
, ![]() ).
).
【解析】(1)解两个函数解析式组成的方程组即可求解;(2)过点P作PG⊥DF于点G,易证△PDG≌△ADE,点P作PH⊥CA于点H,可以证明H是AC的中点,则H的坐标即可求得,进而求得P的坐标,进而求得k的值;(3)Rt△PMC≌Rt△PQR,则RQ=MC,设NR=NC=a,则R(﹣a﹣2,a),代入y=﹣ ![]() x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.
x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
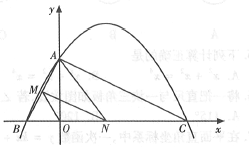
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,若点
,若点![]() 在线段
在线段![]() 上运动(不与点
上运动(不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 面积最大时,求N点的坐标;
面积最大时,求N点的坐标;
(3)连接![]() ,在(2)的结论下,求
,在(2)的结论下,求![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
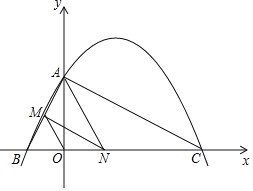
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:

根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com