
【题目】已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形. 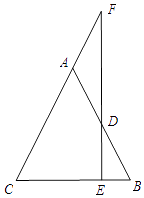
【答案】解:∵AB=AC,
∴∠B=∠C(等边对等角).
∵DE⊥BC于E,
∴∠FEB=∠FEC=90°,
∴∠B+∠EDB=∠C+∠EFC=90°,
∴∠EFC=∠EDB(等角的余角相等).
∵∠EDB=∠ADF(对顶角相等),
∴∠EFC=∠ADF.
∴△ADF是等腰三角形
【解析】先根据等腰三角形的性质得出∠B=∠C,再由等角的余角相等得出∠EFC=∠EDB,进而可得出∠EFC=∠ADF,由此可得出结论.
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.


科目:初中数学 来源: 题型:
【题目】计算题
(1)﹣20+(﹣14)﹣(﹣18)﹣13
(2)0﹣(﹣ ![]() )
)
(3)(﹣1)100×5+(﹣2)4÷4
(4)![]() ÷
÷ ![]() ﹣
﹣ ![]() ×(﹣6)
×(﹣6)
(5)(﹣10)4+[(﹣4)2﹣(3+32)×2]
(6)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣24).
)×(﹣24).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为( )
A.0.845×104亿元
B.8.45×103亿元
C.8.45×104亿元
D.84.5×102亿元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于点A(-4,0)、B(6,0)两点,与y轴交于点C.
与x轴交于点A(-4,0)、B(6,0)两点,与y轴交于点C.
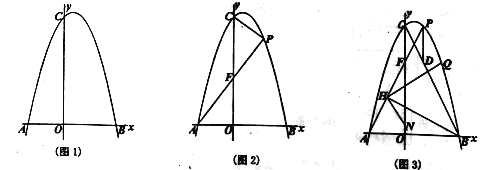
(1)如图l,求抛物线的解析式;
(2)如图2,点P为第一象限抛物线上一点,连接PC、PA,PA交y轴于点F,设点P的横坐标为t,△CPF的面积为S.求S与t的函数关系式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,连接BC,过点P作PD//y轴变BC于点D,点H为AF中点,且点N(0,1),连接NH、BH,将∠NHB绕点H逆时针旋转,使角的一条边H落在射线HF上,另一条边HN变抛物线于点Q,当BH=BD时,求点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 中位数就是一组数据中最中间的一个数
B. 8,9,9,10,10,11这组数据的众数是9
C. 如果x1,x2,x3,…,xn的平均数是x,那么(x1-x)+(x2-x)+…+(xn-x)=0
D. 一组数据的方差是这组数据的平均数的平方
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com