
(本小题10分)已知AB,BC,CD分别与⊙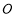 相切于E,F,G三点,且AB∥CD,连接OB,OC.
相切于E,F,G三点,且AB∥CD,连接OB,OC.
(1)如图①,求∠BOC的度数;
(2)如图②,延长CO交⊙O于点M,过点M做MN∥OB交CD于点N,当OB=6,OC=8时,求⊙ 的半径及MN的长.
的半径及MN的长.
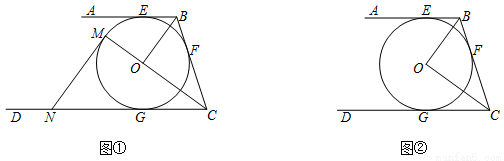
(1)∠BOC=90°;(2)r=4.8;MN=9.6
【解析】
试题分析:(1)根据平行得出∠ABC+∠DCB=180°,根据切线的性质可得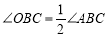 ,
,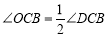 ,得出∠OBC+∠OCB=90°,根据三角形内角和求出∠BOC的度数;(2)连接OF,根据切线得出∠OF⊥BC,根据(1)得出∠BOC=90°,根据勾股定理求出BC的长度,根据面积相等的法则求出OF的长度;根据△MCN和△OCB相似求出MN的长度.
,得出∠OBC+∠OCB=90°,根据三角形内角和求出∠BOC的度数;(2)连接OF,根据切线得出∠OF⊥BC,根据(1)得出∠BOC=90°,根据勾股定理求出BC的长度,根据面积相等的法则求出OF的长度;根据△MCN和△OCB相似求出MN的长度.
试题解析(1)∵AB∥CD, ∴∠ABC+∠DCB=180°∵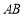 ,
,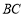 ,
,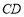 分别与⊙
分别与⊙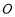 相切于
相切于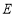 ,
,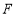 ,
,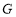 三点,
三点,
∴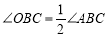 ,
,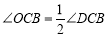 . ∴
. ∴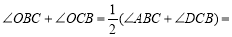 90°.
90°.
∴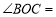 180°-
180°-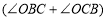 =180°-90°=90°.
=180°-90°=90°.
(2)连接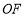 ,∵
,∵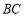 切⊙
切⊙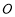 于点
于点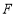 , ∴
, ∴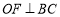 . 由(1)知,
. 由(1)知,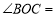 90°,
90°,
∴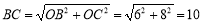 .∵
.∵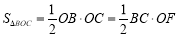 ,∴
,∴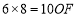 ∴
∴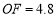 .
.
由(1)知,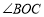 =90°,∴
=90°,∴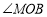 =90°.∵
=90°.∵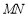 ∥
∥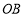 ,∴
,∴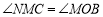 =90°∴
=90°∴ .
.
∵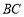 ,
,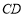 分别切⊙
分别切⊙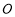 于点
于点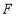 ,
,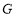 ,∴
,∴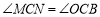 .∴△
.∴△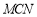 ∽△
∽△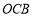 .
.
∴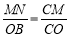 . 即
. 即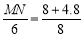 . ∴
. ∴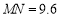 .
.
考点:切线的性质、勾股定理、三角形相似.
考点分析: 考点1:圆 圆,圆的有关性质与圆的有关计算是近几年各地中考命题的重点内容。题型以填空题,选择题和解答题为主,也有以阅读理解,条件开放,结论开放探索题作为新的题型,分值一般是6-12分,难易度为中,考察内容:①圆的有关性质的应用。垂径定理是重点。② 直线和圆,圆和圆的位置关系的判定及应用。③弧长,扇形面积,圆柱,圆锥的侧面积和全面积的计算④圆与相似三角形,三角函数的综合运用以及有关的开放题,探索题。突破方法:①熟练掌握圆的有关行政,掌握求线段,角的方法,理解概念之间的相互联系和知识之间的相互转化。②理解直线和原的三种位置关系,掌握切线的性质和判定的歌,会根据条件解决圆中的动态问题。③掌握有两圆半径的和或差与圆心距的大小关系来盘底的那个两个圆的位置关系,对中考试题中常出现的阅读理解题,探索题,要灵活运用圆的有关性质,进行合理推理与计算。④掌握弧长,扇形面积计算公式。⑤理解圆柱,圆锥的侧面展开图⑥对组合图形 的计算要灵活运用计算方法解题。 试题属性

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年福建省洛江区八年级上学期期末质量检测数学试卷(解析版) 题型:计算题
(11分)已知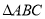 中,
中,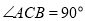 ,
,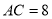 ,
,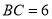 .在射线
.在射线 上取一点
上取一点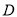 ,使得
,使得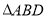 为等腰三角形,这样的三角形有几个?请你求
为等腰三角形,这样的三角形有几个?请你求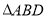 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市和平区九年级下学期结课质量调查数学试卷(解析版) 题型:填空题
如图,在正方形ABCD中,点E,F分别在边BC,CD上,若AE=4,EF=3,AF=5,则正方形ABCD的面积等于 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com