
(9分)如图,AB是 的直径,点D在
的直径,点D在 上,∠DAB=45°,BC∥AD,CD∥AB.
上,∠DAB=45°,BC∥AD,CD∥AB.
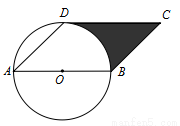
(1)、判断直线CD与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)、若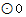 的半径为1,求图中阴影部分的面积(结果保留π).
的半径为1,求图中阴影部分的面积(结果保留π).
(1)、相切;(2)、 .
.
【解析】
试题分析:(1)、连接OD,根据OA=OD,∠ODA=45°得出∠AOD=90°,根据CD∥AB得出∠ODC=90°,从而说明切线;(2)、首先求出梯形OBCD的面积,然后利用梯形的面积减去扇形OBD的面积求出阴影部分的面积.
试题解析:(1)直线CD与⊙O相切. 理由如下:
连接OD. ∵OA=OD,∠DAB=45°,∴∠ODA=45°.
∴∠AOD=90°. 又∵CD∥AB, ∴∠ODC=∠AOD=90°,即OD⊥CD.
又∵点D在⊙O上, ∴直线CD与⊙O相切.
(2)、∵BC∥AD,CD∥AB, ∴ 四边形ABCD是平行四边形.∴CD=AB=2.
∴梯形OBCD的面积=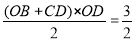
∴图中阴影部分的面积=梯形OBCD的面积-扇形OBD的面积=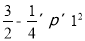 =
=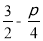 .
.
考点:切线的判定、扇形的面积计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如果只用正三角形作平面镶嵌(要求镶嵌的正三角形的边与另一正三角形有边重合),则在它的每一个顶点周围的正三角形的个数为( )
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
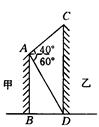
如图1—49所示,两建筑物的水平距离为24 m,从A点测得D点的俯角为60°,测得C点的仰角 为40°,求这两座建筑
为40°,求这两座建筑 物的高.(
物的高.(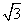 ≈1.732,ta
≈1.732,ta n 40°≈0.8391,精确到0.01 m)
n 40°≈0.8391,精确到0.01 m)
查看答案和解析>>
科目:初中数学 来源: 题型:
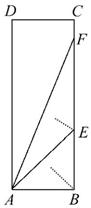
小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°的角的正切值是( )
A. +1 B. +1 C.2.5 D. 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省中山市九年级下学期开学检测数学试卷(解析版) 题型:解答题
(7分)关于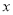 的方程为
的方程为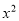 +(m+2)x+2m-1=0.
+(m+2)x+2m-1=0.
(1)、证明:方程有两个不相等的实数根.
(2)、是否存在实数m,使方程的两个实数根互为相反数?若存在,求出m的值及两个实数根;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省中山市九年级下学期开学检测数学试卷(解析版) 题型:填空题
如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”. 则半径为2的“等边扇形”的面积为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:解答题
如图,AB是⊙O的直径,AM、BN分别切⊙O于点A、B,CD交AM,BN于点D、C,DO平分∠ADC.
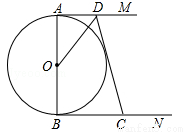
(1)求证:CD是⊙O的切线;
(2)若AD=4,BC=9,求⊙O的半径R.
查看答案和解析>>
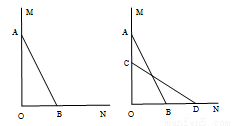
科目:初中数学 来源:2014-2015学年江苏常州西藏民族中学八年级上学期期末联考数学试卷(解析版) 题型:解答题
(本题6分)如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AO上,这时梯足B到墙底端O的距离为0.7米, 如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com