
 =60km/h,
=60km/h,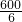 =100km/h;
=100km/h; ,
,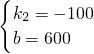 ,
, ,
,
 时,S=600-(60+100)x=-160x+600,
时,S=600-(60+100)x=-160x+600, ≤x<6时,S=(60+100)x-600=160x-600,
≤x<6时,S=(60+100)x-600=160x-600, ;
; 时,-160x+600=200,
时,-160x+600=200, ,
, ≤x<6时,160x-600=200,
≤x<6时,160x-600=200, 小时,然后分①0≤x<
小时,然后分①0≤x< 时,两车的距离为两地间的距离减去两车行驶的路程;②
时,两车的距离为两地间的距离减去两车行驶的路程;② ≤x<6时,两车的距离为两车行驶的路程减去两地间的距离;③6≤x≤10时,两车间的距离为客车行驶的路程;然后利用两点法作一次函数图象作出函数图象即可;
≤x<6时,两车的距离为两车行驶的路程减去两地间的距离;③6≤x≤10时,两车间的距离为客车行驶的路程;然后利用两点法作一次函数图象作出函数图象即可;

科目:初中数学 来源: 题型:
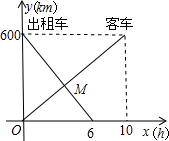 距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:
距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
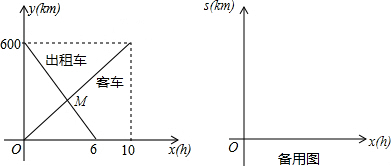
 (2013•黄石)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示:
(2013•黄石)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
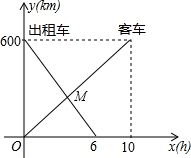 (2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:
(2013•婺城区一模)一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,在行驶过程中,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两地行驶的时间为x小时,y1、y2关于x的函数图象如图所示:
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,在行驶过程中,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两地行驶的时间为x小时,y1、y2关于x的函数图象如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com