
足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑其它因素),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.
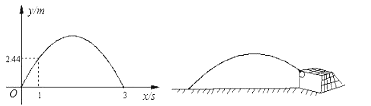
(1)求y关于x的函数解析式;
(2)足球的飞行高度能否达到4.88 m?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44 m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要在几s内到球门的左边框?
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源:山东省临沂市2019届九年级数学上第一次月考试卷(九月_第21、22章) 题型:解答题
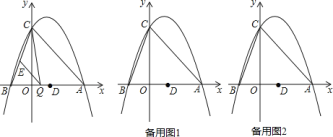
如图,抛物线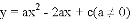 与
与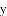
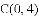
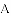
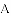
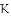
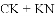
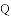
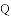
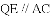
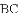
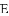
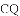
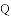
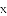

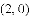

查看答案和解析>>
科目:初中数学 来源:数学人教版2019届九年级上册22.1.4 y=ax2+bx+c的图象和性质 同步训练 题型:单选题
二次函数y=ax2+bx-1(a≠0)的图象经过点(1,-3),则代数式1+a+b的值为( )
A. -3 B. -1 C. 2 D. 5
查看答案和解析>>
科目:初中数学 来源:数学人教版2019届九年级上册22.3 实际问题与二次函数(2) 同步训练 题型:单选题
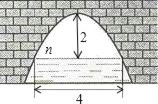
如图,图中是抛物线形拱桥,当拱顶离水面2m时水面宽4m.水面下降1m,水面宽度为( )
A. 2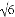 m B. 2
m B. 2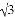 m C.
m C. 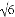 m D.
m D. 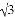 m
m
查看答案和解析>>
科目:初中数学 来源:数学人教版2019届九年级上册22.3 实际问题与二次函数(2) 同步训练 题型:单选题
有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
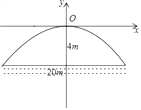
A. 2.76米 B. 6.76米 C. 6米 D. 7米
查看答案和解析>>
科目:初中数学 来源:2019届数学人教版九年级上册22.3 实际问题与二次函数(1) 同步训练 题型:填空题
2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系 ,则羽毛球飞出的水平距离为 米.
,则羽毛球飞出的水平距离为 米.

查看答案和解析>>
科目:初中数学 来源:2019届数学人教版九年级上册22.3 实际问题与二次函数(1) 同步训练 题型:单选题
某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A. y=(x﹣40)(500﹣10x) B. y=(x﹣40)(10x﹣500)
C. y=(x﹣40)[500﹣10(x﹣50)] D. y=(x﹣40)[500﹣10(50﹣x)]
查看答案和解析>>
科目:初中数学 来源:数学2019届人教版九年级上册22.2.1 抛物线与x轴的交点 同步训练 题型:填空题
二次函数y=ax2+bx+c(a≠0)的图象与____的交点的横坐标x1,x2就是一元二次方程ax2+bx+c=0(a≠0)的两个____.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
(题文)(问题引领)
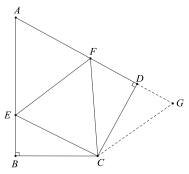
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.
(探究思考)
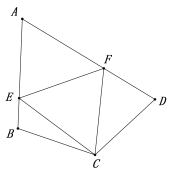
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF=  ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.
(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com