
如图一次函数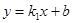 的图象与反比例函数
的图象与反比例函数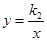 的图象交于点A
的图象交于点A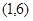 ,B(3,a).
,B(3,a).
(1)求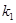 、
、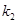 的值;
的值;
(2)直接写出一次函数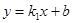 的值大于反比例函数
的值大于反比例函数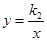 的值时x的取值范围:
的值时x的取值范围:
;
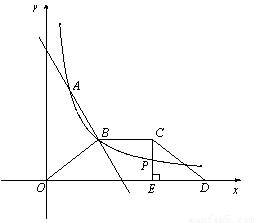
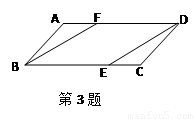
(3)如图,等腰梯形OBCD中,BC//OD,OB=CD,OD边在x 轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象 交于点P,当点P为CE的中点时,求梯形OBCD的面积.
(1)k1=-2,k2=6(2)1<x<3 或 x<0(3)12
【解析】(1)把A 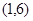 代入
代入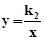 得:k2=6 ∴
得:k2=6 ∴  (1分)
(1分)
把B(3,a)代入 得:a=2 ∴B(3,
得:a=2 ∴B(3,
2) (1分)
把B(3,2)A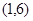 分别代入
分别代入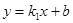 得:
得: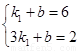
解得: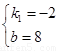
∴k1=-2 (2分)
(2)1<x<3 或 x<0 (2分)
(3) 等腰梯形OBCD中,BC//OD,OB=CD,OD边在x轴上且B(3,2)
设C(a,2) (1分)
∵CE⊥OD于点E,CE和反比例函数的图象交于点P, 点P为CE的中点,∴P(a,1) (1分)
把P(a,1)代入 得:a=6 ∴C(6,2) ∴BC=3
(1分)
得:a=6 ∴C(6,2) ∴BC=3
(1分)
又∵OD=9 CE=2 (1分)
∴S梯形OBCD=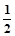 ×(9+3)×2=12 (2分)
×(9+3)×2=12 (2分)
(1)先把A(1,6)代入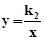 可求出k2=6,则反比例函数的解析式
可求出k2=6,则反比例函数的解析式 ,然后把B(3,a)代入
,然后把B(3,a)代入 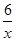 得a=2,确定B点坐标为(3,2),再利用待定系数法确定一次函数的解析式,从而得到k1的值;
得a=2,确定B点坐标为(3,2),再利用待定系数法确定一次函数的解析式,从而得到k1的值;
(2)观察图象得到当x<0或1<x<3时,一次函数的图象在反比例函数图象的上方;
(3)设C(t,2),过B作BF⊥x轴于F点,由点P为CE的中点得到P(t,1),又由点P在反比例函数 的图象上,易得C点坐标为(6,2),再利用OB=CD,OD边在x轴上且B(3,2),得到BC=3,ED=OF=3,则OD=OF+EF+ED=9,而CE=2,然后根据梯形的面积公式计算即可.
的图象上,易得C点坐标为(6,2),再利用OB=CD,OD边在x轴上且B(3,2),得到BC=3,ED=OF=3,则OD=OF+EF+ED=9,而CE=2,然后根据梯形的面积公式计算即可.
 |


科目:初中数学 来源: 题型:解答题
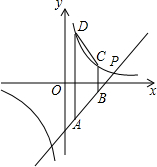 如图,已知反比例函数y=
如图,已知反比例函数y= 的图象和一次函数y=kx-7的图象都经过点P(m,2).
的图象和一次函数y=kx-7的图象都经过点P(m,2).查看答案和解析>>
科目:初中数学 来源:2012届山西省临汾市平阳中学九年级下学期第一次月考试卷(带解析) 题型:解答题
如图一次函数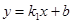 的图象与反比例函数
的图象与反比例函数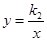 的图象交于点A
的图象交于点A ,B(3,a).
,B(3,a).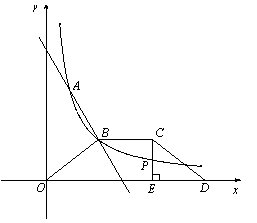
(1)求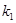 、
、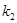 的值;
的值;
(2)直接写出一次函数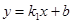 的值大于反比例函数
的值大于反比例函数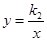 的值时x的取值范围:
的值时x的取值范围:
;
(3)如图,等腰梯形OBCD中,BC//OD,OB=CD,OD边在x 轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象 交于点P,当点P为CE的中点时,求梯形OBCD的面积.
查看答案和解析>>
科目:初中数学 来源:2012年苏教版初中数学八年级下9.3反比例函数的应用练习卷(解析版) 题型:解答题
如图,一次函数的图象与x轴、y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、第三象限,且OA=OB= AC=BD,试求一次函数和反比例函数的解析式.
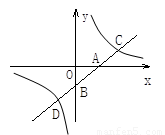
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com