
分析 原式括号中两项通分并利用同分母分式的减法法则计算,除数分子利用完全平方公式分解因式,再利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分得到最简结果,代入a的值,即可求出结果.
解答 解:原式=$\frac{{{a^2}-1}}{a}÷\frac{{{{(a-1)}^2}}}{a}$
=$\frac{(a+1)(a-1)}{a}×\frac{a}{{{{(a-1)}^2}}}$=$\frac{a+1}{a-1}$,
∵a=$\sqrt{2}$+1,
∴$({a-\frac{1}{a}})÷\frac{{{a^2}-2a+1}}{a}$=$\frac{\sqrt{2}+1+1}{\sqrt{2}+1-1}$=2$+2\sqrt{2}$.
点评 此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
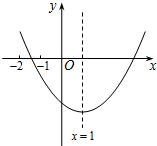 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③b=-2a;④9a+3b+c<0. 其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc>0;③b=-2a;④9a+3b+c<0. 其中,正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
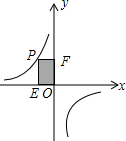 如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )
如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为5.这个函数的解析式为( )| A. | y=$\frac{5}{x}$ | B. | y=-$\frac{5}{x}$ | C. | y=$\frac{10}{x}$ | D. | y=-$\frac{x}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com