
分析 (1)不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离2为高,所以三角形BOP的面积是一个常数;
(2)△ABC的面积已知,把△ABP的面积用a表示,就可以得到关于a的方程,解方程可以求出a.
解答 解:(1)如图,
不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离1为高,
∴S△BOP=$\frac{1}{2}×1×2$=1为常数;
(2)AB=$\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$,
${S}_{△ABC}=\frac{1}{2}×\sqrt{10}×\sqrt{10}$=5,
当点P在第四象限时,a<0,
∵S△ABO$\frac{1}{2}×3×1$=$\frac{3}{2}$,S△APO=-$\frac{3}{2}$a,
∴S△ABP=S△ABO+S△APO-S△BOP=S△ABC=5,
即$\frac{3}{2}-\frac{3}{2}a-1$=5,
解得a=-3,
当点P在第一象限时,同理可得a=7,
综上所述,a的值为-3或7.
点评 此题主要考查了坐标与图形的性质,解决本题的关键是探讨变化三角形的面积,结合了方程的知识,解方程就可以求出a.


科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
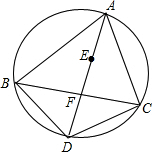 已知,如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D,弦AD交弦BC于点F.
已知,如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D,弦AD交弦BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com