
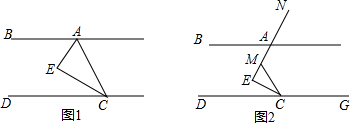
分析 (1)先根据平行线的性质得出∠BAE+∠CAE+∠DCE+∠ACE=180°,再由∠AEC=90°可知∠CAE+∠ACE=90°,故可得出∠BAE+∠DCE=90°,由CE平分∠ACD可知∠DCE=∠ACE,故∠ACE+∠BAE=90°,由此可得出结论;
(2)延长AE交DG于点F,根据平行线的性质可得出∠BAE=∠AFC,由∠AEC=90°可知∠CEF=90°,故可得出∠AFC+∠ECD=90°,再根据∠MCE=∠ECD,MCE+∠ECD=180°-∠MCG可得出结论.
解答 (1)证明:∵AB∥CD,
∴∠BAE+∠CAE+∠DCE+∠ACE=180°.
∵∠AEC=90°,
∴∠CAE+∠ACE=90°,
∴∠BAE+∠DCE=90°.
∵CE平分∠ACD,
∴∠DCE=∠ACE,
∴∠ACE+∠BAE=90°,
∴∠BAE=∠CAE,即AE平分∠BAC;
(2)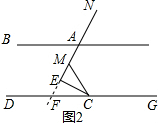 ∠BAE=$\frac{1}{2}$∠MCG.
∠BAE=$\frac{1}{2}$∠MCG.
证明:∵延长AE交DG于点F,
∵AB∥CD,
∴∠BAE=∠AFC.
∵∠AEC=90°,
∴∠CEF=90°,
∴∠AFC+∠ECD=90°.
∵∠MCE=∠ECD,MCE+∠ECD=180°-∠MCG,
∴∠BAE+$\frac{1}{2}$(180°-∠MCG)=90°,即∠BAE=$\frac{1}{2}$∠MCG.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
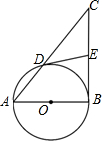 如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.
如图,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
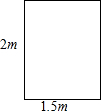 如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽
如图,是一扇高为2m,宽为1.5m的门框,现有3块薄木板,尺寸如下:①号木板长3m,宽| A. | ①号 | B. | ②号 | C. | ③号 | D. | 均不能通过 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
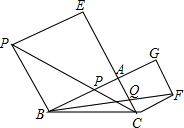 如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.
如图,在△ABC中,∠BAC=90°,分别以AB,AC为边向外作正方形ABDE和ACFG,连接DC,FB,分别交AB,AC于P,Q.求证:AP=AQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com