Question

20．如图，锐角△ABC内接于⊙O，E为CB延长线上一点，连接AE交⊙O于点D，∠E=∠BAC，连接BD．
（1）求证：∠DBE=∠ABC；
（2）若∠E=45°，BE=3，BC=5，求△AEC的面积．

Answer 1

分析 （1）连接BD，根据等腰三角形的性质和三角形的外角的性质即可得到结论；
（2）根据相似三角形的性质得到AC=2$\sqrt{10}$，过C作CF⊥AE于F，根据等腰直角三角形的性质得到CF=EF=4$\sqrt{2}$，由勾股定理得到AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=2$\sqrt{2}$，得到AE=6$\sqrt{2}$，根据三角形的面积公式即可得到结论．

解答 （1）证明：连接BD，
∴∠DBE=∠DAC，
∵∠ABC=∠E+∠DAB，
∵∠E=∠BAC，
∴∠ABC=∠CAB+∠DAB=∠DAC，
∴∠DBE=∠ABC；

（2）解：∵∠E=∠BAC，∠C=∠C，
∴△ACE∽△BCA，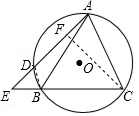
∴$\frac{AC}{CE}=\frac{BC}{AC}$，即$\frac{AC}{5+3}$=$\frac{5}{AC}$，
∴AC=2$\sqrt{10}$，
过C作CF⊥AE于F，
∵∠E=45°，
∴△CEF是等腰直角三角形，
∴CF=EF=4$\sqrt{2}$，
∵AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=2$\sqrt{2}$，
∴AE=6$\sqrt{2}$，
∴S_△ACE=$\frac{1}{2}$AE•CF=$\frac{1}{2}×$6$\sqrt{2}$×4$\sqrt{2}$=24．

点评 本题考查了相似三角形的判定和性质，等腰直角三角形的判定和性质，三角形面积的计算，正确的作出辅助线是解题的关键．