
 x+m(0<m≤1)的图象为直线l,直线l绕原点O旋转180
x+m(0<m≤1)的图象为直线l,直线l绕原点O旋转180 °后得直线l′,△ABC三个顶点的坐标分别为A(-
°后得直线l′,△ABC三个顶点的坐标分别为A(- ,-1)、B(
,-1)、B( ,-1)、C(0,2).
,-1)、C(0,2). x平移时,判断△ABC介于直线l,l′之间部分的面积是否改变?若不变请指出来;若改变请直接写出面积变化的范围.(本小题不必说明理由)
x平移时,判断△ABC介于直线l,l′之间部分的面积是否改变?若不变请指出来;若改变请直接写出面积变化的范围.(本小题不必说明理由) 解:(1)∵一次函数y=
解:(1)∵一次函数y= x+m(O<m≤1)与x轴交于点M(-
x+m(O<m≤1)与x轴交于点M(- m,0),与y轴交于点N(0,m),
m,0),与y轴交于点N(0,m), m,0),与y轴交于点N(0,-m),
m,0),与y轴交于点N(0,-m), -m;
-m; ,-1)、C(0,2),∴直线AC的解析式为y=
,-1)、C(0,2),∴直线AC的解析式为y= x+2,
x+2, x+m,直线l′的解析式为y=
x+m,直线l′的解析式为y= -m,
-m, ,-1)、B(
,-1)、B( ,-1)、C(0,2),
,-1)、C(0,2), ,
, ∴△ABC是等边三角形.
∴△ABC是等边三角形. x+m=-1,x=
x+m=-1,x= ,∴E(
,∴E( ,-1),BE=
,-1),BE= -
- =
= ,
, x-m=-1,x=
x-m=-1,x= ,∴H(
,∴H( ,-1),BH=
,-1),BH= -
- =
=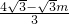 ,
, ,
,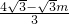 .
. m,0),点N(0,m),∴MN=
m,0),点N(0,m),∴MN= .
. =
= m,∴2OD=m,
m,∴2OD=m, (EF+GH)•2OD=
(EF+GH)•2OD= m(
m( +
+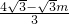 )=
)= ,
, ∵
∵ >0,
>0, ;
; x平移,由平移的知识可知面积不变;
x平移,由平移的知识可知面积不变; .
. .
. x平移时,面积不变;沿y=x平移时,面积改变,设其面积为S'.显然,如果△ABC与l、l′没有交点,则面积S′取最小值0;由于m=1时,△ABC介于直线l,l′之间的部分是一个梯形,l与l′之间的距离是1,即梯形的高是1,则当EF+GH取最大值时,S′有最大值,此时直线l与l′中有一条过点C,且F、G落在△ABC的同一边上,可求S′=
x平移时,面积不变;沿y=x平移时,面积改变,设其面积为S'.显然,如果△ABC与l、l′没有交点,则面积S′取最小值0;由于m=1时,△ABC介于直线l,l′之间的部分是一个梯形,l与l′之间的距离是1,即梯形的高是1,则当EF+GH取最大值时,S′有最大值,此时直线l与l′中有一条过点C,且F、G落在△ABC的同一边上,可求S′= ,则0≤S'≤
,则0≤S'≤ .
.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com