
| A. | 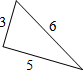 | B. | 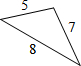 | C. | 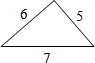 | D. |  |
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
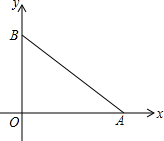 在平面直角坐标系中,已经A(8,0),B(0,6)
在平面直角坐标系中,已经A(8,0),B(0,6)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
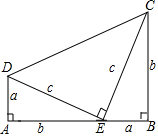 用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)(a+b)=a2-b2 | C. | a2+b2=c2 | D. | c2-a2=(c-a)(c+a) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
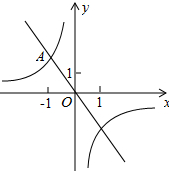 如图,在平面直角坐标系中,一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,n)
如图,在平面直角坐标系中,一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,n)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
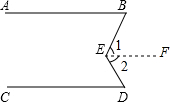 完成正确的证明如图,已知AB∥CD,求证:∠BED=∠B+∠D
完成正确的证明如图,已知AB∥CD,求证:∠BED=∠B+∠D查看答案和解析>>
科目:初中数学 来源: 题型:填空题
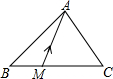 如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AM}=\overrightarrow{b}$,那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a},\overrightarrow{b}$表示)
如图,在△ABC中,点M在边BC上,MC=2BM,设向量$\overrightarrow{AB}=\overrightarrow{a}$,$\overrightarrow{AM}=\overrightarrow{b}$,那么$\overrightarrow{BC}$=3$\overrightarrow{b}$-3$\overrightarrow{a}$(结果用$\overrightarrow{a},\overrightarrow{b}$表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com