
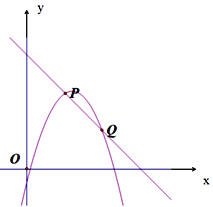
【题目】已知:如图,直线y=-x+b与抛物线y=-x2+4x+c交于P、Q两点.
(1)若点P坐标为(1,2),
①求c的值;
②求Q点坐标;
(2)若 P、Q两点的横坐标分别为m、n,且0<m<n.分别过点P、Q作PA、QB垂直于x轴,垂足分别为点A、B.当△AOP≌△BQO时.
①求m+n的值;
②求证:![]()
【答案】(1)①c=-1;②(4,-1);(2)①m+n=5;②证明见解析
【解析】
(1)将P(1,2)代入即可解题,(2)根据全等得P(m,n),Q(n,m),联立方程即可求解,再利用根的判别式即可判定c的取值范围.
解:(1)将P(1,2)代入y=-x2+4x+c中得c=-1, 将P(1,2)代入y=-x+b中得b=3,
∴直线为y=-x+3,抛物线为y=-x2+4x-1,
联立方程组![]() 解得:
解得:![]() 或
或![]() ,
,
∴Q(4,-1);
(2)①如下图,∵△AOP≌△BQO,
∴OA=BQ,AP=OB,即P(m,n),Q(n,m),
∵P,Q两点都在函数y=-x2+4x-1上,即, ![]()
(2)-(1)得m+n=5,
②∵m=5-n,将m代入方程中得n2-5n+5-c=0,
∴△![]() 0,解得c
0,解得c![]() ,当c
,当c![]() 时P,Q重合,直线与抛物线只有一个交点,
时P,Q重合,直线与抛物线只有一个交点,
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
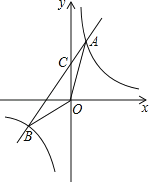
【题目】如图,已知一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班的各5名学生的成绩,它们分别为:
九(1)班 :96,92,94,97,96;
九(2)班 :90,98,97,98,92.
通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 |
九(1)班 | 95 | a | 96 |
九(2)班 | 95 | 97 | b |
(1)a= , b = ;
(2)计算两个班所抽取的学生艺术成绩的方差,判断哪个班学生的艺术成绩比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
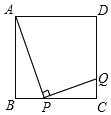
【题目】如图,在正方形ABCD中,AB=4,点P、Q分别在直线CB与射线DC上(点P不与点C、点B重合),且保持∠APQ=90°,CQ=1,则线段BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )

A.①③④ B.①②③ C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明周末要乘坐公交车到植物园游玩,从地图上查找路线发现,几条线路都需要换乘一次.在出发站点可选择空调车A、空调车B、普通车a,换乘站点可选择空调车C,普通车b、普通车c,且均在同一站点换乘.空调车投币2元,普通车投币1元.
(1)求小明在出发站点乘坐空调车的概率;
(2)求小明到达植物园恰好花费3元公交费的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红和小白想利用所学的概率知识设计一个摸球游戏,在一个不透明的袋子中装入完全相同的4个小球,把它们分别编号为:2、3、4、5,.两人先后从袋中随机摸出一个球,若摸出的两个小球上的数字和是奇数则小红胜,否则小白胜.请判断这个游戏是否公平?并用概率知识说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com