
 (a2+b2)
(a2+b2) (a2+b2)
(a2+b2) (a+b)2
(a+b)2 ab
ab absinC,那么当∠C=90°时,△ABC的面积最大,且最大值是
absinC,那么当∠C=90°时,△ABC的面积最大,且最大值是 ab,再结合完全平方公式(a-b)2≥0,可得
ab,再结合完全平方公式(a-b)2≥0,可得 ab≤
ab≤ (a2+b2),
(a2+b2),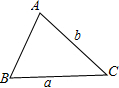 解:∵△ABC的两边长时a、b,
解:∵△ABC的两边长时a、b, absinC,
absinC, ab,
ab, ab≤
ab≤ (a2+b2),
(a2+b2), (a2+b2),
(a2+b2), (a2+b2)>
(a2+b2)> (a2+b2),
(a2+b2), (a+b)2=
(a+b)2= [
[ (a2+b2)+
(a2+b2)+ ab]≥
ab]≥ ab,
ab, ab<
ab< ab,
ab,

 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源:2011年黑龙江省哈尔滨市中考调研测试数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com