Question

10．下列条件能判断△ABC与△DEF相似的有（　　）
（1）∠A=∠D，∠E=∠C；（2）$\frac{AB}{AC}=\frac{DE}{DF}，∠A=∠D$；（3）$\frac{AB}{DE}=\frac{BC}{EF}，∠A=∠D$
（4）$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$； （5）∠A=∠D，$\frac{BC}{DF}=\frac{2}{3}$．

• A． 2个
• B． 3个
• C． 4个
• D． 5个

Answer 1

分析 直接根据三角形相似的判定方法分别判断得出答案．

解答 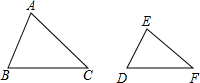解：（1）∠A=∠D，∠E=∠C，可以得出△ABC∽△DFE，故正确；
（2）$\frac{AB}{AC}=\frac{DE}{DF}，∠A=∠D$，可以得出△ABC∽△DEF，故正确；
（3）$\frac{AB}{DE}=\frac{BC}{EF}，∠A=∠D$，不是两边成比例且夹角相等，故此选项错误；
（4）$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$，可得出△ABC∽△DEF，故正确； 
（5）∠A=∠D，$\frac{BC}{DF}=\frac{2}{3}$，无法得出相似三角形，故此选项错误．
故选：B．

点评 此题主要考查了相似三角形的判定，关键是掌握三角形相似的判定方法：（1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；（2）三边法：三组对应边的比相等的两个三角形相似；（3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；（4）两角法：有两组角对应相等的两个三角形相似．