练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．在实数：3.14，$\frac{22}{7}$，$\sqrt{7}$，$\root{3}{-8}$，$\sqrt{{2}^{2}}$，π中，无理数是$\sqrt{7}$，π．

    分析 根据无理数的定义即可判定求解．

    解答 解：3.14是有理数，$\frac{22}{7}$是有理数，$\sqrt{7}$是无理数，$\root{3}{-8}$=-2是有理数，$\sqrt{{2}^{2}}$=2是有理数，π是无理数，
    故答案为：$\sqrt{7}$，π

    点评 此题主要考查了无理数的定义．注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

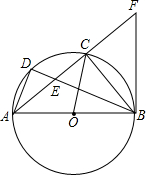    19．如图，在△ABC内接于⊙O，AB为直径，D是$\widehat{AC}$上的点，BD交AC于点E，过点B作⊙O的切线与AC的延长线交于点F，已知AB=5，sin∠CAB=$\frac{3}{5}$．
    （1）求CF的长；
    （2）若CE=$\frac{9}{4}$，求证：AD∥OC；
    （3）在满足（2）的条件下，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

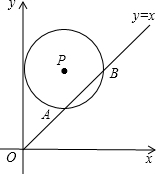    20．如图，在平面直角坐标系中，与y轴相切的⊙P的圆心是（2，a）且（a＞2），
    函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$，则a的值是（　　）
    A．2$\sqrt{3}$B．2+$\sqrt{3}$C．2+$\sqrt{2}$D．2$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列化简或计算正确的是（　　）
    A．$\sqrt{（-\sqrt{3}）^{2}}$=-$\sqrt{3}$B．$\sqrt{1\frac{1}{49}}$=1+$\frac{1}{7}$=$\frac{8}{7}$C．（$\sqrt{6}-\sqrt{3}$）2=9-2$\sqrt{3}$D．$\sqrt{24}$÷（-$\frac{1}{2}$$\sqrt{6}$）=-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知△ABC的三个内角、三条边长如图，则甲、乙、丙三个三角形中，和△ABC全等的图形是乙和丙．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列说法正确的是（　　）
    A．两个形状和大小相同的图形可看作其中一个是另一个经过平移得到的
    B．边长相等的两个正方形一定可以通过平移得到
    C．周长和面积均相等的两个图形一定由平移得到
    D．由平移得到的两个图形的对应点连线相互平行或在同一条直线上

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

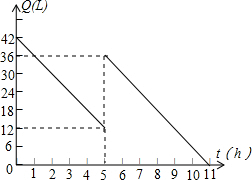    1．某机动车出发前油箱内有油42L，行驶若干小时后，途中在加油站加油若干升．油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：
    （1）机动车行驶5h后加油，途中加油24升；
    （2）根据图形计算，机动车在加油前的行驶中每小时耗油多少升？
    （3）如果加油站距目的地还有400km，车速为60km/h，要到达目的地，油箱中的油是否够用？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

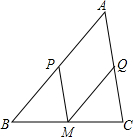    18．如图，在△ABC中，P、M、Q分别是AB、BC、AC的中点．
    （1）求证：四边形APMQ是平行四边形；
    （2）直接写出当△ABC满足什么条件时，四边形APMQ是菱形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．我市为绿化城区，计划购买甲、乙两种树苗共计500棵，甲种树苗每棵50元，乙种树苗每棵80元．设购买甲种树苗x棵，则
    （1）购买乙种树苗为（500-x）棵；
    （2）如果购买两种树苗共用28000元，那么甲、乙两种树苗各买了多少棵？
    （3）市绿化部门研究决定，购买树苗的钱数不得超过34000元，应如何选购树苗？

    查看答案和解析>>

    同步练习册答案