
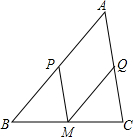
 如图,在△ABC中,P、M、Q分别是AB、BC、AC的中点.
如图,在△ABC中,P、M、Q分别是AB、BC、AC的中点.分析 (1)由已知条件得出PM是△ABC的中位线,得出PM∥AC,PM=$\frac{1}{2}$AC,同理:QM∥AB,QM=$\frac{1}{2}$AB,即可得出结论;
(2)由PM=$\frac{1}{2}$AC,QM=$\frac{1}{2}$AB,得出PM=QM,即可得出四边形APMQ是菱形.
解答 (1)证明:∵P、M、分别是AB、BC的中点,
∴PM是△ABC的中位线,
∴PM∥AC,PM=$\frac{1}{2}$AC,
同理:QM∥AB,QM=$\frac{1}{2}$AB,
∴四边形APMQ是平行四边形;
(2)得当AB=AC时,四边形APMQ是菱形;理由如下:
解:由(1)得:PM=$\frac{1}{2}$AC,QM=$\frac{1}{2}$AB,
∵AB=AC,
∴PM=QM,
∴四边形APMQ是菱形.
点评 本题考查了三角形中位线定理、平行四边形的判定、菱形的判定、等腰三角形的性质;熟练掌握三角形中位线定理,并能进行推理论证是解决问题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:选择题
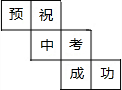 一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )
一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )| A. | 预 | B. | 祝 | C. | 成 | D. | 功 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 代入消元法 | B. | (1)×29-(2)×26,先消去x | ||
| C. | (1)×26-(2)×29,先消去y | D. | (1)+(2),两方程相加 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
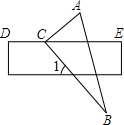 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )| A. | 135° | B. | 60° | C. | 50° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000名运动员是总体 | B. | 抽取的100名运动员是样本 | ||
| C. | 样本容量是100 | D. | 每个运动员是个体 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com