
【题目】如图,在△MBN中,BM=6,点A、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则ABCD的周长是( ) 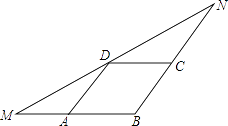
A.24
B.18
C.16
D.12
【答案】D
【解析】解:∵四边形ABCD为平行四边形, ∴AD=BC,DC=AB,AB∥DC,AD∥BN,
∴∠N=∠ADM,∠M=∠NDC,
∵∠NDC=∠MDA,
∴∠N=∠NDC,∠M=∠MDA,∠M=∠N,
∴CN=DC,AD=MA,NB=MB,
∴平行四边形ABCD的周长是 BM+BN=6+6=12,
所以答案是:D.
【考点精析】本题主要考查了平行四边形的性质和相似三角形的判定与性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
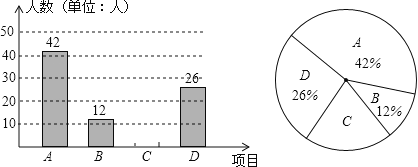
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一元一次方程解下列应用题
据国家统计局发布的数据显示,在我国的664个城市中,按水资源可分为暂不缺水城市、一般缺水城市和严重缺水城市三类.其中,暂不缺水城市比严重缺水城市的4倍少50个,一般缺水城市是严重缺水城市的2倍.
(1)求严重缺水城市有多少个?
(2)为了解决缺水的问题,国家启动了多个水利工程,缓解了部分严重缺水城市的情况,使一般性缺水城市的数目是严重缺水城市的9倍,求现在一般性缺水的城市有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘,由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)
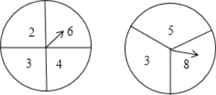
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能判定一个四边形是菱形的条件是( )
A. 对角线互相平分且相等 B. 对角线互相垂直且相等
C. 对角线互相垂直且对角相等 D. 对角线互相垂直,且一条对角线平分一组对角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列给出的条件中,能识别一个四边形是菱形的是( )
A. 有一组对边平行且相等,有一个角是直角
B. 两组对边分别相等,且有一组邻角相等
C. 有一组对边平行,另一组对边相等,且对角线互相垂直
D. 有一组对边平行且相等,且有一条对角线平分一个内角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m. 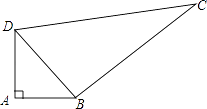
(1)试判断△BCD的形状;
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com