
【题目】(1)若![]() ,则
,则![]()
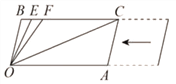
(2)如图,CB∥OA,∠B=∠A=108°,E、F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF,若平行移动AC,当∠OCA= 时。可以使∠OEB=∠OCA。
【答案】(1)-2014 (2)54°
【解析】分析: (1)方程移项变形后,得:a2-4a=1,a2=4a+1,再将代数式中的a3化为2a2a=2a(4a+1),达到降次的目的,合并同类项后,最后提取公因式,代入可得结论;
(2)由于BC∥OA,∠B=108°,易求∠AOB,而OE、OC都是角平分线,从而可求∠COE;设∠OCA=α,∠AOC=x,根据三角形的外角性质、三角形的内角和定理、平行线的性质可得,α+x=72°,36°+x=α,解即可.
详解: :(1)a2+4a-1=0,
移项得:a2+4a=1,a2=1-4a,
则2a3+11a2+10a-2017,
=2a(1-4a)+11a2+10a-2017,
=2a-8a+11a2+10a-2017,
=3a2+12a-2017,
=3(a2+4a)-2017,
=3×1-2017,
=-2014;
(2))∵CB∥OA,
∴∠BOA+∠B=180°,
∴∠BOA=180°-108°=72°,
∵∠FOC=∠AOC,OE平分∠BOF,
∴∠EOC=∠EOF+∠FOC=![]() ∠BOF+
∠BOF+![]() ∠FOA=
∠FOA=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ×72°=36°;
×72°=36°;
在平行移动AC的过程中,存在∠OEB=∠OCA,
设∠OCA=α,∠AOC=x,
∵∠OEB=∠COE+∠OCB=36°+x,
∠ACO=72°-x,
∴α=72°-x,36°+x=α,
72-x=36+x,
∴x=18°,α=54°.
即:当∠OCA=54度时.可以使∠OEB=∠OCA.
点睛: 本题考查了因式分解的应用、平行线的性质、角平分线的定义及平移的性质,两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】若关于![]() 的二元一次方程组
的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)若上述方程组的解是等腰三角形的腰和底边的长,且这个等腰三角形周长为9,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我县中考的体育测试成绩改为等级制,即把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格.我县5月份举行了全县九年级学生体育测试.现从中随机抽取了部分学生的体育成绩,并将其绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: 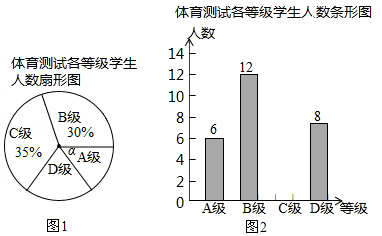
(1)本次抽样测试的学生人数是;
(2)图1中∠α的度数是 , 并把图2条形统计图补充完整;
(3)该县九年级有学生9000名,如果全部参加这次中考体育科目测试,请估算不及格的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )

A. y=x+12 B. y=0.5x+12
C. y=0.5x+10 D. y=x+10.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
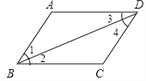
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180-∠A,∠2+∠4=180―∠C,∠A=∠C,
∴ ∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是(_____)
A. ∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 B. ∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C. ∠A∶∠B∶∠C∶∠D=2∶3∶3∶2 D. ∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知分式![]() .
.
(1)当____时,分式的值等于零;
(2)当____时,分式无意义;
(3)当___且___时分式的值是正数;
(4)当____时,分式的值是负数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com