
【题目】已知点 A(x,y),若 xy=0,那么点 A 在___________________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,∠D=∠C=90°,E是DC的中点,AE平分∠DAB,∠DEA=28°,则∠ABE的度数是( )

A. 62° B. 31° C. 28° D. 25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线c1: ![]() 沿x轴翻折,得到抛物线c2 , 如图1所示.
沿x轴翻折,得到抛物线c2 , 如图1所示.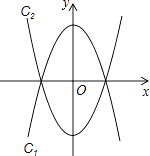
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.
①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若![]() ,则
,则![]()
(2)如图,CB∥OA,∠B=∠A=108°,E、F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF,若平行移动AC,当∠OCA= 时。可以使∠OEB=∠OCA。
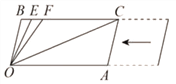
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90,当点D在线段BC上时(与点B不重合),如图2,线段CF,BD所在直线位置关系为 ,数量关系为 .
(2)如果AB=AC,∠BAC=90,当点D在线段BC的延长线时,如图3,(1)中的结论是否仍然成立,并说明理由。
(3)如果AB=AC,∠BAC是钝角,点D在线段BC上,当∠ABC满足什么条件时,CF⊥BC(点C、F不重合)画出图形,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
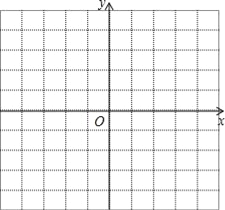
【题目】如图的平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,分别得到A1、B1、C1,依次连接A1,B1,C1,各点,请写出A1、B1、C1的坐标并画出△A1B1C1,并判断所得三角形A1B1C1与三角形ABC的大小、形状和位置有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,分别得到A2、B2、C2,依次连接A2,B2,C2,各点,请写出A2、B2、C2的坐标并画出△A2B2C2,并判断所得三角形A2B2C2与三角形ABC的大小、形状和位置有什么关系?
(3)求△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个底面直径为5 cm,高为18 cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,四边形OECB的顶点坐标分别是:B(2,5),C(8,5),E(10,0),点P(x,0)是线段OE上一点,设四边形BPEC的面积为S.

(1)过点C作CD⊥x轴于点E,则CD= , 用含x的代数式表示PE= .
(2)求S与x的函数关系.
(3)当S=30时,直接写出线段PE与PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com