
����Ŀ����������c1�� ![]() ��x�ᷭ�ۣ��õ�������c2 �� ��ͼ1��ʾ��
��x�ᷭ�ۣ��õ�������c2 �� ��ͼ1��ʾ��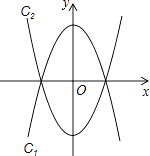
��1����ֱ��д��������c2�ı���ʽ��
��2���ֽ�������c1����ƽ��m����λ���ȣ�ƽ�ƺ�õ��������ߵĶ���ΪM����x��Ľ������������ΪA��B����������c2����Ҳƽ��m����λ���ȣ�ƽ�ƺ�õ��������ߵĶ���ΪN����x��Ľ������������ΪD��E��
�ٵ�B��D���߶�AE�����ȷֵ�ʱ����m��ֵ������ƽ�ƹ����У��Ƿ�����Ե�A��N��E��MΪ������ı����Ǿ��ε����Σ������ڣ��������ʱm��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺y= ![]() x2��
x2�� ![]()
��2��
�⣺����ͼ1��� ![]() x2+
x2+ ![]() =0����x1=��1��x2=1
=0����x1=��1��x2=1
������c1��x�������������������1��0������1��0����
��A����1��m��0����B��1��m��0����
ͬ���ɵã�D����1+m��0����E��1+m��0����
��AD= ![]() AEʱ��
AEʱ��
����1+m��������1��m��= ![]() [��1+m��������1��m��]��
[��1+m��������1��m��]��
��m= ![]() ��
��
��BD= ![]() AEʱ��
AEʱ��
����1+m������1��m��= ![]() [��1+m��������1��m��]��
[��1+m��������1��m��]��
��m=2��
�ʵ�B��D���߶�AE�����ȷֵ�ʱ��m= ![]() ��2��
��2��
�ڴ��ڣ�
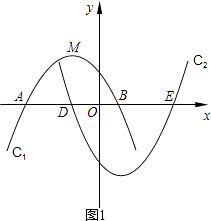
���ɣ���ͼ2������AN��NE��EM��MA��

������ɵã�M����m�� ![]() ����N��m����
����N��m���� ![]() ����
����
��M��N����ԭ��O�Գƣ�
��OM=ON��
��A����1��m��0����E��1+m��0����
��A��E����ԭ��O�Գƣ�
��OA=OE
���ı���ANEMΪƽ���ı��Σ�
��AM2=����m+1+m��2+�� ![]() ��2=4��
��2=4��
ME2=��1+m+m��2+�� ![]() ��2=4m2+4m+4��
��2=4m2+4m+4��
AE2=��1+m+1+m��2=4m2+8m+4��
��AM2+ME2=AE2����4+4m2+4m+4=4m2+8m+4��
��m=1��
��ʱ��AME��ֱ�������Σ��ҡ�AME=90�㣮
�൱m=1ʱ���Ե�A��N��E��MΪ������ı����Ǿ��Σ�
����������1�����ݷ��۵����ʿ�������c2�ı���ʽ����2�������������c1��x��������������꣬�ֵ�AD= ![]() AEʱ����BD=
AEʱ����BD= ![]() AEʱ�������������⣻�ڴ��ڣ����ɣ���ͼ2������AN��NE��EM��MA�����ݾ��ε��ж����ɵó���
AEʱ�������������⣻�ڴ��ڣ����ɣ���ͼ2������AN��NE��EM��MA�����ݾ��ε��ж����ɵó���
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AB C��DE��EF���ۣ�����A��B�����ڵ�O������EA��EB�غ����߶�EO������CDO+��CFO=98�㣬���C�Ķ���Ϊ�� ��
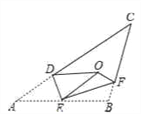
A. 40�� B. 41�� C. 42�� D. 43��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�����������ϵ�λ����ͼ��ʾ������OΪԭ�㣬��A��Ӧ��������Ϊ��4����B��Ӧ��������Ϊ6��
��1������P�ӵ�A��������ÿ��2����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�루t��0����
�ٵ�t=1ʱ��AP�ij�Ϊ�� ������P��ʾ��������Ϊ�� ����
�ڵ�PB=2ʱ����t��ֵ��
��2���������P��ÿ��6����λ���ȵ��ٶȴ�O�������˶�����A��B�ֱ���ÿ��1����λ���Ⱥ�ÿ��3����λ���ȵ��ٶ������˶���������ͬʱ��������ô��������PA=2PB��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬����OB��OC������AB��OB��OC��AC���е�D��E��F��G�������ᣬ�õ��ı���DEFG��

��1����֤���ı���DEFG��ƽ���ı��Σ�
��2����MΪEF���е㣬OM=3����OBC����OCB���࣬��DG�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��F�ڶԽ���AC�ϣ���AE=CF����֤��
��1��DE=BF��
��2���ı���DEBF��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֽ���ʽ��
��1��![]() ��2��
��2�� ![]()
��3��![]() ��4��
��4�� ![]()
��5��![]() ��6��
��6�� ![]()
��7��![]() 8��
8��![]()
��9��![]() ��10��
��10��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Сѧ�����ҵ��й��Ρ������У�ijУ�Բ���ѧ������һ������Ϊ������ϲ����ͼ�顱�ĵ�������ͼ���Ϊ�ס��ҡ����������࣬ѧ���ɸ����Լ��İ�����ѡ����һ�ࡣѧУ���ݵ������������ͳ�ƣ��������˲�����������ͳ��ͼ������ͳ��ͼ��ͼ��
������ϲ����ͼ�顱��������ͳ��ͼ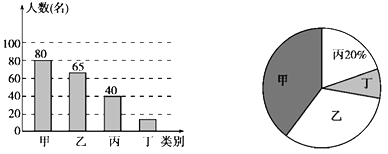
������ͼ����Ϣ������������⣺
��1�����ι������� ��ѧ����
��2���������ѧ���У���ϲ������ͼ����� ������ϲ������ͼ�������ռ���α����������� %��
��3������ϲ������ͼ���ѧ���У�Ů������������������1.5����������ѧУ����ѧ��1500����������Ƹ�У��ϲ������ͼ���Ů���������ֱ��ж�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com