
【题目】分解因式:
(1)![]() (2)
(2) ![]()
(3)![]() (4)
(4) ![]()
(5)![]() (6)
(6) ![]()
(7)![]() 8)
8)![]()
(9)![]() (10)
(10)![]()
【答案】(1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ![]() ;(10)
;(10) ![]() .
.
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
(3)直接利用完全平方公式进行分解;
(4)首先提取公因式3,再利用完全平方公式进行分解;
(5)首先提取公因式-a,再利用完全平方公式进行分解;
(6)首先利用平方差公式进行分解,再利用完全平方公式进行分解;
(7)首先利用完全平方公式进行分解,再利用完全平方公式进行二次分解;
(8)首先利用平方差公式进行分解,再利用完全平方公式进行分解;
(9)首先提取公因式n2,再利用完全平方公式进行二次分解;
(10)首先提取公因式-2axn-1,再利用完全平方公式进行二次分解.
试题解析:(1)原式=-(4a2-4a+1)=-(2a-1)2;
(2)原式=-y(4x2-12xy+9y2 )=-y(2x-3y)2;
(3)原式=(3x-3y+1)2;
(4)原式=3(1-2x+x2)=3(1-x)2;
(5)原式=-a(1-a)2;
(6)原式=(x+y)2(x-y)2;
(7)原式=(a2-2ab+b2)(a2+2ab+b2)=(a+b)2(a-b)2;
(8)原式=(x2+9-6x)(x2+9+6x)=(x+3)2(x-3)2;
(9)原式=n2(![]() +n)2;
+n)2;
(10)原式=-2axn-1(1-6x+9x2)=-2axn-1(1-3x)2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将抛物线c1: ![]() 沿x轴翻折,得到抛物线c2 , 如图1所示.
沿x轴翻折,得到抛物线c2 , 如图1所示.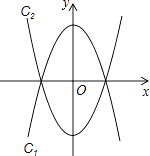
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.
①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90,当点D在线段BC上时(与点B不重合),如图2,线段CF,BD所在直线位置关系为 ,数量关系为 .
(2)如果AB=AC,∠BAC=90,当点D在线段BC的延长线时,如图3,(1)中的结论是否仍然成立,并说明理由。
(3)如果AB=AC,∠BAC是钝角,点D在线段BC上,当∠ABC满足什么条件时,CF⊥BC(点C、F不重合)画出图形,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
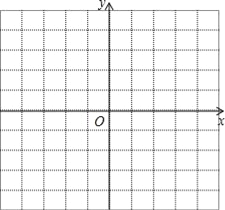
【题目】如图的平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,分别得到A1、B1、C1,依次连接A1,B1,C1,各点,请写出A1、B1、C1的坐标并画出△A1B1C1,并判断所得三角形A1B1C1与三角形ABC的大小、形状和位置有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,分别得到A2、B2、C2,依次连接A2,B2,C2,各点,请写出A2、B2、C2的坐标并画出△A2B2C2,并判断所得三角形A2B2C2与三角形ABC的大小、形状和位置有什么关系?
(3)求△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个底面直径为5 cm,高为18 cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班组织班队活动,班委会准备买一些奖品。.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件。
【1】有多少种购买方案?请列举所有可能的结果;
【2】从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com