
【题目】如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为_____.

【答案】![]()
【解析】
作AM⊥BC于E,由角平分线的性质得出![]() ,设AC=2x,则BC=3x,由线段垂直平分线得出MN⊥BC,BN=CN=
,设AC=2x,则BC=3x,由线段垂直平分线得出MN⊥BC,BN=CN=![]() x,得出MN∥AE,得出
x,得出MN∥AE,得出![]() ,NE=x,BE=BN+EN=
,NE=x,BE=BN+EN=![]() x,CE=CNEN=
x,CE=CNEN=![]() x,再由勾股定理得出方程,解方程即可得出结果.
x,再由勾股定理得出方程,解方程即可得出结果.
解:作AM⊥BC于E,如图所示:

∵CD平分∠ACB,
∴![]() ,
,
设AC=2x,则BC=3x,
∵MN是BC的垂直平分线,
∴MN⊥BC,BN=CN=![]() x,
x,
∴MN∥AE,
∴![]() ,
,
∴NE=x,
∴BE=BN+EN=![]() x,CE=CNEN=
x,CE=CNEN=![]() x,
x,
由勾股定理得:AE2=AB2BE2=AC2CE2,
即52(![]() x)2=(2x)2(
x)2=(2x)2(![]() x)2,
x)2,
解得:x=![]() ,
,
∴AC=2x=![]() ;
;
故答案为![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】如图,经过点B(0,2)的直线y=kx+b与x轴交于点C,与正比例函数y=ax的图象交于点A(﹣1,3)
(1)求直线AB的函数的表达式;
(2)直接写出不等式(kx+b)﹣ax<0的解集;
(3)求△AOC的面积;
(4)点P是直线AB上的一点,且知△OCP是等腰三角形,写出所有符合条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,要求每件销售价格不得高于27元,并将所得利润捐给贫困母亲。经试验发现,若每件按22元的价格销售时,每天能卖出42件;若每件按25元的价格销售时,每天能卖出33件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润![]() 最大,最大利润是多少?
最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:

求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级学生的体育成绩,从全年级学生中随机抽取部分学生进行“双飞”跳绳测试,结果分为A,B,C,D四个等级,请跟进两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该学校七年级共有400名学生,请你估计该学校七年级学生中“双飞”跳绳测试结果为D等级的学生有多少名.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值
解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,t2=81,∴t=±9因为2m2+n2≥0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
已知实数x,y满足(4x2+4y2+3)(4x2+4y2﹣3)=27,求x2+y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )

A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如图所示(部分信息未给出):
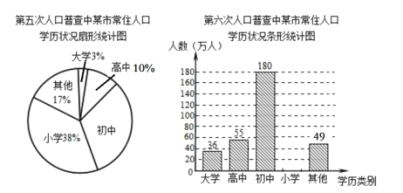
解答下列问题:
(1)求第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)求第五次人口普查中该市常住人口每万人中具有初中学历的人数;
(3)第六次人口普查结果与第五次相比,每万人中初中学历的人数增加了多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com