
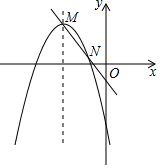
 如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为(0,2).
如图,已知抛物线y=-x2+px+q的对称轴为x=-3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(-1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为(0,2). 分析 首先,求得抛物线的解析式,根据抛物线解析式求得M的坐标;欲使△PMN的周长最小,MN的长度一定,所以只需(PM+PN)取最小值即可.然后,过点M作关于y轴对称的点M′,连接M′N,M′N与y轴的交点即为所求的点P(如图1);过点M作关于x轴对称的点M′,连接M′N,则只需M′N与x轴的交点即为所求的点P(如图2).
解答 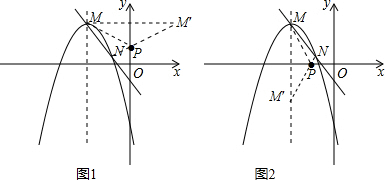 解:如图,∵抛物线y=-x2+px+q的对称轴为x=-3,点N(-1,1)是抛物线上的一点,
解:如图,∵抛物线y=-x2+px+q的对称轴为x=-3,点N(-1,1)是抛物线上的一点,
∴$\left\{\begin{array}{l}{-\frac{p}{2}=-3}\\{-1-p+q=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{p=-6}\\{q=-4}\end{array}\right.$.
∴该抛物线的解析式为y=-x2-6x-4=-(x+3)2+5,
∴M(-3,5).
∵△PMN的周长=MN+PM+PN,且MN是定值,所以只需(PM+PN)最小.
如图1,过点M作关于y轴对称的点M′,连接M′N,M′N与y轴的交点即为所求的点P.则M′(3,5).
设直线M′N的解析式为:y=ax+t(a≠0),
则$\left\{\begin{array}{l}{5=3a+t}\\{1=-a+t}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{t=2}\end{array}\right.$,
故该直线的解析式为y=x+2.
当x=0时,y=2,即P(0,2).
同理,如图2,过点M作关于x轴对称的点M′,连接M′N,则只需M′N与x轴的交点即为所求的点P(-$\frac{4}{3}$,0).
如果点P在y轴上,则三角形PMN的周长=4$\sqrt{2}$+MN;如果点P在x轴上,则三角形PMN的周长=2$\sqrt{10}$+MN;
所以点P在(0,2)时,三角形PMN的周长最小.
综上所述,符合条件的点P的坐标是(0,2).
故答案为(0,2).
点评 本题考查了轴对称-最短路线问题,二次函数的性质,待定系数法求一次函数的解析式,一次函数图象上点的坐标特征.在求点P的坐标时,一定要注意题目要求是“要在坐标轴上找一点P”,所以应该找x轴和y轴上符合条件的点P,不要漏解,这是同学们容易忽略的地方.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:填空题
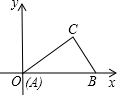 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合.随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
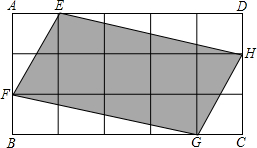 如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.
如图,将矩形ABCD分成15个大小相等的正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积为$\frac{5}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}b}{3}$ | B. | $\frac{a+1}{4}$ | C. | 0 | D. | $\frac{{a}^{2}+b}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
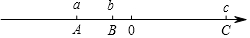 如图,点A、B、C在数轴上表示的数a、b、c,且满足:(b+2)2+(c-24)2=0,且多项式x|a+3|y2-ax3y+xy2-1是五次四项式.
如图,点A、B、C在数轴上表示的数a、b、c,且满足:(b+2)2+(c-24)2=0,且多项式x|a+3|y2-ax3y+xy2-1是五次四项式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com