Question

已知点E、F在△ABC的边AB所在的直线上，且AE=BF，FH∥FG∥AC，FH、EG分别交边BC所在的直线于点H、G。
（1）如图1，如果点E、F在边AB上，那么EG+FH=AC；
（2）如图2，如果点E在边AB上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是 _________ ；
（3）如图3，如果点E在AB的反向延长线上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是_____________。
对（1）（2）（3）三种情况的结论，请任选一个给予证明。

Answer 1

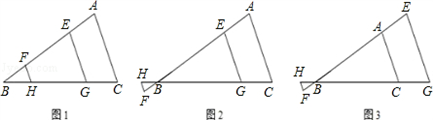
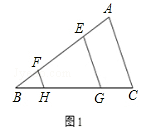
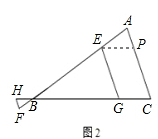
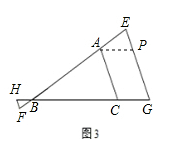
（1）证明：∵FH∥EG∥AC， ∴∠BFH=∠BEG=∠A，△BFH∽△BEG∽△BAC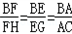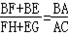， ∴．∴， 又∵BF=EA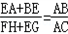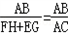， ∴， ∴， ∴AC=FH+EG； （2）线段EG、FH、AC的长度的关系为：EG+FH=AC， 证明（2）：过点E作EP∥BC交AC于P， ∵EG∥AC， ∴四边形EPCG为平行四边形， ∴EG=PC， ∵HF∥EG∥AC， ∴∠F=∠A，∠FBH=∠ABC=∠AEP， 又∵AE=BF， ∴△BHF≌△EPA， ∴HF=AP， ∴AC=PC+AP=EG+HF， 即EG+FH=AC； （3）线段EG、FH、AC的长度的关系为：EG﹣FH=AC， 如图，过点A作AP∥BC交EG于P， ∵EG∥AC， ∴四边形APGC为平行四边形， ∴AC=PG， ∵HF∥EG∥AC， ∴∠F=∠E，∠FBH=∠ABC=∠PAE， 又∵AE=BF， ∴△BHF≌△EPA， ∴HF=EP， ∴AC=EG﹣EP=EG﹣HF， 即EG﹣FH=AC。