
【题目】如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D地边AC上,点E、F在边AB上,点G在边BC上。
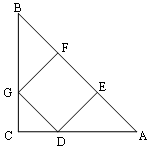
(1)求证:△ADE≌△BGF;
(2)若正方形DEFG的面积为16cm2,求AC的长。
【答案】(1)证明见解析;(2)AC=![]() cm.
cm.
【解析】
试题分析:(1)先根据等腰直角三角形的性质得出∠B=∠A=45°,再根据四边形DEFG是正方形可得出∠BFG=∠AED,故可得出∠BGF=∠ADE=45°,GF=ED,由全等三角形的判定定理即可得出结论;
(2)过点C作CH⊥AB于点H,由正方形DEFG的面积为16cm2可求出其边长,故可得出AB的长,在Rt△ADE中,根据勾股定理可求出AD的长,再由相似三角形的判定定理得出△ADE∽△ACG,由相似三角形的对应边成比例即可求出AC的长.
试题解析:(1)∵△ABC是等腰直角三角形,∠C=90°,
∴∠B=∠A=45°,
∵四边形DEFG是正方形,
∴∠BFG=∠AED=90°,
故可得出∠BGF=∠ADE=45°,GF=ED,
∵在△ADE与△BGF中,
 ,
,
∴△ADE≌△BGF(ASA);
(2)过点C作CH⊥AB于点H,
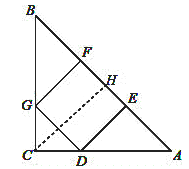
∵正方形DEFG的面积为16cm2,
∴DE=AE=4cm,
∴AB=3DE=12cm,
∵△ABC是等腰直角三角形,CH⊥AB,
∴AH=![]() AB=
AB=![]() ×12=6cm,
×12=6cm,
在Rt△ADE中,
∵DE=AE=4cm,
∴AD=![]() cm,
cm,
∵CH⊥AB,DE⊥AB,
∴CH∥DE,
∴△ADE∽△ACH,
∴![]() ,
,![]() ,
,
解得AC=![]() cm.
cm.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
![]()
(1)数轴上点B对应的数是______.
(2)经过几秒,恰好使AM=2BN?
(3)经过几秒,点M、点N分别到原点O的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瓦甸科星化工有限公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家三口国庆节随旅游团去九寨沟旅游,共花费人民币5600元,他把旅途费用支出情况制成了如下的统计图.请你根据统计图解决下列问题:
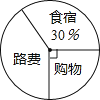
(1)哪一部分支出的费用占整个支出的![]() ?
?
(2)小明一家在食宿上用去多少元?
(3)小明一家支出的路费共多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com