练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】等腰三角形中，,于点D.

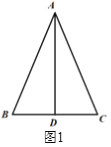
    (1)如图1，当∠C=3∠BAD，求∠C的度数.

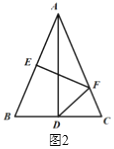
    (2)如图2，EF垂直平分AB，交于点F，连结DF，当时，求证：DF=DC.

    【答案】(1)∠C=67.5°；(2)证明见解析.

    【解析】

    解：（1）设∠BAD=x，

    ∵∠C=3∠BAD，

    ∴∠C=3x，

    ∵AB=AC，AD⊥BC，

    ∴AD⊥BC，

    ∴∠ADC=90°，

    ∴∠DAC+∠C=90°，

    ∴x+3x=90，

    ∴x=22.5，

    ∴∠C=67.5°；

    （2）如图，连接BF，

    ∵EF平分AB，

    ∴AF=BF，

    ∴∠ABF=∠BAF=45°，

    ∴∠BFC=∠ABF+∠BAF=90°，

    ∵AB=AC，AD⊥BC，

    ∴D为BC中点，

    ∵∠BFC=90°，D为BC中点，

    ∴，

    ∴DF=DC；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】随机抽取某市一年（以365天计）中的30天的日平均气温状况统计如下：温度（）

    温度（）

    10

    14

    18

    22

    26

    30

    32

    天数

    3

    5

    5

    7

    6

    2

    2

    请根据上述数据回答下列问题：

    （1）估计该城市年平均气温大约是多少？

    （2）上表中的温度数据的中位数是_______众数是_________；

    （3）计算该城市一年中约有几天的日平均气温为?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知正比例函数与一次函数的图像交于点A.

    （1）求点A的坐标；

    （2）设x轴上一点P（a，b），过点P作x轴的垂线（垂线位于点A的右侧），分别交和的图像于点B、C，连接OC，若BC=OA，求△OBC的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，等腰Rt△OAB中，∠AOB=90°，等腰Rt△EOF中，∠EOF=90°，连结AE、BF．

    求证：（1）AE=BF；（2）AE⊥BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有6个质地和大小均相同的球，每个球只标有一个数字，将标有3,4,5的三个球放入甲箱中，标有4,5,6的三个球放入乙箱中．

    (1)小宇从甲箱中随机模出一个球，求“摸出标有数字是3的球”的概率；

    (2)小宇从甲箱中、小静从乙箱中各自随机摸出一个球，若小宇所摸球上的数字比小静所摸球上的数字大1，则称小宇“略胜一筹”．请你用列表法(或画树状图)求小宇“略胜一筹”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，-1）．

    （1）请以y轴为对称轴，画出与△ABC对称的△A1B1C1，并直接写出点A1、B1、C1的坐标；

    （2）△ABC的面积是 ．

    （3）点P（a+1，b-1）与点C关于x轴对称，则a= ，b= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

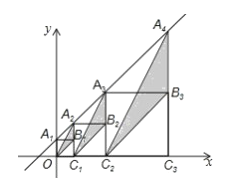
    【题目】在直角坐标系中，直线与y轴交于点，按如图方式作正方形、、、…，点、、、…在直线上，点、、、…，在x轴上，图中阴影部分三角形的面积从左到右依次记为、、、…，则_______，________.（用含n的代数式表示，n为正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

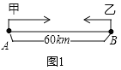
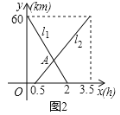
    【题目】A、B两地相距60km,甲从A地去B地，乙从B地去A地，图中l1、l2分别表示甲、乙两人离B地的距离y（km）与甲出发时间x（h）的函数关系图象.

    （1）根据图象，直接写出乙的行驶速度；

    （2）解释交点A的实际意义；

    （3）甲出发多少时间，两人之间的距离恰好相距5km；

    （4）若用y3（km）表示甲乙两人之间的距离，请在坐标系中画出y3（km）关于时间x（h）的函数关系图象，注明关键点的数据.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

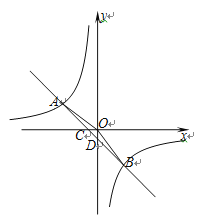
    【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，﹣4），连接AO，AO=5，sin∠AOC=．

    （1）求反比例函数的解析式

    （2）连接OB，求△AOB的面积

    (3) 根据图象直接写出当时，x的取值范围．

    查看答案和解析>>

    同步练习册答案