
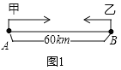
����Ŀ��A��B�������60km,�״�A��ȥB�أ��Ҵ�B��ȥA�أ�ͼ��l1��l2�ֱ��ʾ�ס���������B�صľ���y��km����׳���ʱ��x��h���ĺ�����ϵͼ��.
��1������ͼ��ֱ��д���ҵ���ʻ�ٶȣ�
��2�����ͽ���A��ʵ�����壻
��3���׳�������ʱ�䣬����֮��ľ���ǡ�����5km��
��4������y3��km����ʾ��������֮��ľ��룬��������ϵ�л���y3��km������ʱ��x��h���ĺ�����ϵͼ��ע���ؼ��������.
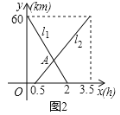
���𰸡���1��20km/h����2����A��ʵ���������ڼ׳���1.4Сʱʱ������������������ʱ����B��18km����3�����׳���1.3h��1.5hʱ������֮��ľ���ǡ�����5km����4��������.
��������
��1����2�����ݺ���ͼ���е����ݿ������ҵ���ʻ�ٶȣ��������A�����꣬˵����A��ʵ�����壻
��3�����ݣ�1���еĺ�������ʽ�������г���Ӧ�ĵ�ʽ���Ӷ�������ü׳�������ʱ�䣬����֮��ľ���ǡ�����5km��
��4�����ݺ���ͼ���е����ݿ������y3��km������ʱ��x��h�����εĺ�������ʽ���Ӷ����Ի�����Ӧ��ͼ��
�⣺��1����ͼ��ɵã�
�ҵ���ʻ�ٶ�Ϊ��60�£�3.5-0.5��=20km/h.
��2����l1��Ӧ�ĺ�������ʽΪy1=k1x+b1�� ��
��
��l1��Ӧ�ĺ�������ʽΪy1=-30x+60��
��l2��Ӧ�ĺ�������ʽΪy2=k2x+b2�� ����
����
��l2��Ӧ�ĺ�������ʽΪy2=20x-10��
��![]()
����A��������1.4��18����
���A��ʵ���������ڼ׳���1.4Сʱʱ������������������ʱ����B��18km��
��3��������ɵã�
|��-30x+60��-��20x-10��|=5��
��ã�x1=1.3��x2=1.5��
�𣺵��׳���1.3h��1.5hʱ������֮��ľ���ǡ�����5km��
��4��������ɵã�
��0��x��0.5ʱ��y3=-30x+60��
��0.5��x��1.4ʱ��y3=y1-y2=��-30x+60��-��20x-10��=-50x+70��
��1.4��x��2ʱ��y3=y2-y1=��20x-10��-��-30x+60��=50x-70��
��2��x��3.5ʱ��y3=20x-10��
y3��km������ʱ��x��h���ĺ�����ϵͼ����ͼ2��ʾ��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
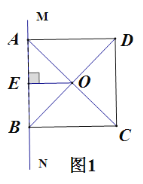
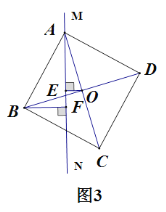
����Ŀ��������ABCD�ı�AB��ֱ��MN�ϣ�O��AC��BD�Ľ��㣬��O��OE��MN�ڵ�E��
��1����ͼ1���߶�AB��OE֮���������ϵΪ ������ֱ������ۣ�
��2����֤��Aʼ����ֱ��MN�ϣ�������ABCD�Ƶ�A��ת![]() ��0��
��0��![]() ��90�㣩������B��BF��MN�ڵ�F��
��90�㣩������B��BF��MN�ڵ�F��
�� ��ͼ2������O��B�������ֱ��MN�Ҳ�ʱ���Բ����߶�AF��BF��OE֮�����������������ϵ����˵�����ɣ�
�� ��ͼ3������O��B����ֱ���ֱ��MN����ʱ����ʱ���н����Ƿ���Ȼ�����أ�����������ֱ��д�����ۣ�������������д���仯��Ľ��۲�֤����
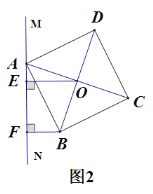
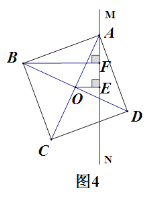
�� ��������ABCD�Ƶ�A��ת����ͼ4��λ��ʱ���߶�AF��BF��OE֮���������ϵΪ ������ֱ������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
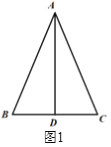
����Ŀ������������![]() �У�
�У�![]() ,
,![]() �ڵ�D.
�ڵ�D.
(1)��ͼ1������C=3��BAD�����C�Ķ���.
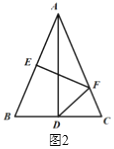
(2)��ͼ2��EF��ֱƽ��AB����![]() �ڵ�F������DF����
�ڵ�F������DF����![]() ʱ����֤��DF=DC.
ʱ����֤��DF=DC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ����ABC������![]() ��
��![]() ��
��![]() .
.

��1��������ABC ���� y ��ĶԳ�ͼ��![]() ����д������
���������
��A ���� x ��ԳƵĵ�����Ϊ_____________��
�� B ���� y ��ԳƵĵ�����Ϊ_____________��
�� C ����ԭ��ԳƵĵ�����Ϊ_____________��
��2���������ϵ�ÿ��С�����εı߳�Ϊ 1�����ABC �����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ�������ϵ�У�����y=2x��y=-x��ͼ��ֱ�Ϊֱ��l1��l2�����㣨1��0����x��Ĵ��߽�l2�ڵ�A1������A1��y��Ĵ��߽�l2�ڵ�A2������A2��x��Ĵ��߽�l1�ڵ�A3������A3��y��Ĵ��߽�l2�ڵ�A4���������ν�����ȥ�����A2020������Ϊ_______________
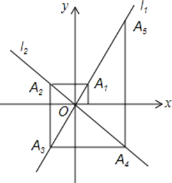
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��![]() ��ƽ�����ཻ�ڵ�E������E��
��ƽ�����ཻ�ڵ�E������E��![]() ��
��![]() �ڵ�F����ôEF�ij�Ϊ�� ��
�ڵ�F����ôEF�ij�Ϊ�� ��
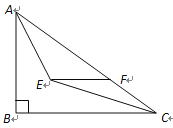
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���kx2+��2k+1��x+2=0��
��1����֤������kȡ�κ�ʵ��ʱ����������ʵ������
��2�������̵���������ƽ���͵���5����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����λ���������������λ������ʮλ����֮��Ϊ��λ���֣������������λ��Ϊ������������������������m�İ�λ�������λ���ֽ���λ�ã����������õ���������m�ġ�������������156��һ��������������651��156�ġ������������ڼ�����![]() �е�|x��y|��0��1ʱ������Ϊ����г����������
�е�|x��y|��0��1ʱ������Ϊ����г����������
��1����λ����Ϊ6�ġ���г������������ ������λ����Ϊ9�ġ���г������������ ����
��2��֤��������һ���������������䡰��������֮��ܱ�11������
��3����֪mΪ������������n��m�ġ�������������m��n�ĺ��ܱ�8��������m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��������ֱ��ڵ�
��������ֱ��ڵ�![]() ��
��![]() �͵�
�͵�![]() ������
������![]() ��ԭ��
��ԭ��![]() ��ʼ��
��ʼ��![]() ������ÿ��
������ÿ��![]() ����λ�����ƶ�������
����λ�����ƶ�������![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() ������ÿ��
������ÿ��![]() ����λ�����ƶ�������
����λ�����ƶ�������![]() ��
��![]() ͬʱ������������
ͬʱ������������![]() ����ԭ��
����ԭ��![]() ʱ����
ʱ����![]() ��
��![]() ֹͣ�˶���
ֹͣ�˶���

![]() ֱ��д�������ߵĽ���ʽ��________��
ֱ��д�������ߵĽ���ʽ��________��
![]() ��
��![]() �����
�����![]() ��
��![]() ���˶�ʱ��
���˶�ʱ��![]() �ĺ�������ʽ����
�ĺ�������ʽ����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ���������������Ƕ��٣�
���������������Ƕ��٣�
![]() ��
��![]() ��������ʱ�������������Ƿ���ڵ�
��������ʱ�������������Ƿ���ڵ�![]() ����
����![]() ���⣩��ʹ
���⣩��ʹ![]() ���������
���������![]() ���������������ڣ����
���������������ڣ����![]() ������ꣻ�������ڣ���˵�����ɣ�
������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com