
【题目】已知关于x的一元二次方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)若方程的两个根的平方和等于5,求k的值.
【答案】(1)详见解析;(2):k=±1.
【解析】
(1)根据方程的系数结合根的判别式,可得出△=(2k﹣1)2≥0,由此可证出:无论k取任何实数时(k≠0),方程总有实数根;
(2)根据根与系数的关系可得x1+x2=﹣![]() 、x1x2=
、x1x2=![]() ,结合x12+x22=5即可得出关于k的一元二次方程,解之即可得出k值.
,结合x12+x22=5即可得出关于k的一元二次方程,解之即可得出k值.
(1)证明:∵方程kx2+(2k+1)x+2=0为一元二次方程,
∴k≠0.
∵△=(2k+1)2﹣4×2k=(2k﹣1)2≥0,
∴无论k取任何实数时(k≠0),方程总有实数根;
(2)解:设方程kx2+(2k+1)x+2=0的两个根为x1、x2,
∴x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
∵x12+x22=(x1+x2)2﹣2x1x2=5,即(﹣![]() )2﹣
)2﹣![]() =5,
=5,
整理,得:k2=1,
解得:k=±1.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
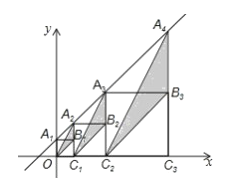
【题目】在直角坐标系中,直线![]() 与y轴交于点
与y轴交于点![]() ,按如图方式作正方形
,按如图方式作正方形![]() 、
、![]() 、
、![]() 、…,点
、…,点![]() 、
、![]() 、
、![]() 、…在直线
、…在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 、…,在x轴上,图中阴影部分三角形的面积从左到右依次记为
、…,在x轴上,图中阴影部分三角形的面积从左到右依次记为![]() 、
、![]() 、
、![]() 、…
、…![]() ,则
,则![]() _______,
_______,![]() ________.(用含n的代数式表示,n为正整数)
________.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
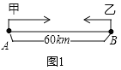
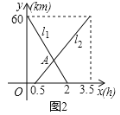
【题目】A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中l1、l2分别表示甲、乙两人离B地的距离y(km)与甲出发时间x(h)的函数关系图象.
(1)根据图象,直接写出乙的行驶速度;
(2)解释交点A的实际意义;
(3)甲出发多少时间,两人之间的距离恰好相距5km;
(4)若用y3(km)表示甲乙两人之间的距离,请在坐标系中画出y3(km)关于时间x(h)的函数关系图象,注明关键点的数据.
查看答案和解析>>
科目:初中数学 来源: 题型:
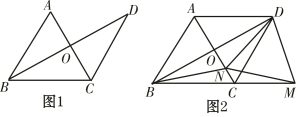
【题目】已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接BD交AC于点O.
(1)如图1,求证:AC垂直平分BD;
(2)如图2,点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN.求证:NB=NM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华同学想测量学校逸夫楼的高度,他站在B点从A处仰望楼顶D,测得仰角为30°,再往逸夫楼的方向前进14米从E处望楼顶,测得仰角为60°,已知小华同学身高(AB)为1.6米,则逸夫楼CD的高度的为( )(![]() ≈1.73)
≈1.73)

A.12.1米B.13.7米C.11.5米D.13.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
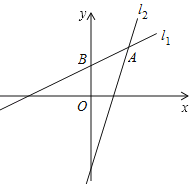
【题目】已知直线l1:y1=![]() x+3经过点A(m,5),与y轴的交点为B;直线l2:y2=kx+b经过点A和C(2,﹣1).
x+3经过点A(m,5),与y轴的交点为B;直线l2:y2=kx+b经过点A和C(2,﹣1).
(1)求直线l2的解析式,并直接写出不等式y1≥y2的解集;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
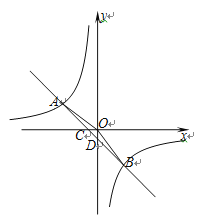
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式
(2)连接OB,求△AOB的面积
(3) 根据图象直接写出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
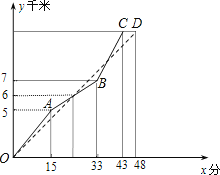
【题目】如图表示甲、乙两名选手在一次自行车越野赛中,路程y(千米)随时间x(分)变化的图象.下面几个结论:①比赛开始24分钟时,两人第一次相遇.②这次比赛全程是10千米.③比赛开始38分钟时,两人第二次相遇.正确的结论为_____(只填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com