练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若一个整数的绝对值小于5，则符合这个条件的整数共有多少个？请你从中选取5个，然后求这5个数的绝对值的和．

    答案：
    解析：

    9个；答案不唯一，如：|－1|＋|0|＋|1|＋|2|＋|3|＝7．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    任何一个正整数n都可以进行这样的分解：n=s×t（s，t是正整数，且s≤t），如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F(n)=
    p
    q
    、例如18可以分解成1×18，2×9，3×6这三种，这时就有F(18)=
    3
    6
    =
    1
    2
    ．给出下列关于F（n）的说法：（1）F(2)=
    1
    2
    ；（2）F(24)=
    3
    8
    ；（3）F（27）=3；（4）若n是一个整数的平方，则F（n）=1．其中正确说法的有
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    任何一个正整数n都可以进行这样的分解：n=s×t（s、t是正整数，且s≤t），如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q（p≤q）是n的最佳分解，并规定F(n)=
    p
    q
    ．例如：18可以分解成1×18，2×9，3×6，这时就有F(18)=
    3
    6
    =
    1
    2
    ．结合以上信息，给出下列关于F（n）的说法：①F(2)=
    1
    2
    ；②F(24)=
    3
    8
    ；③F(27)=
    1
    3
    ；④若n是一个整数的平方，则F（n）=1．其中正确的说法有
    ①③④
    ①③④
    ．（只填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    任何一个正整数n都可以进行这样的分解：n=s×t（s，t是正整数，且s≤t），如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q在n的最佳分解，并规定：F(n)=
    P
    q
    (p≤q)    ．例如24可以分解成1×24，2×12，3×8，4×7这四种，这时就有F(24)=
    4
    6
    =
    2
    3
    ，则：
    （1）有F（36）=
    1
    1
    ．
    （2）给出下列关于F（n）的说法：
    ①F(2)=
    1
    2
    ②F(18)=
    1
    2
    ；③F（27）=3；④若n是一个整数的平方，则F（n）=1
    上述4个说法正确的有
    ①②④
    ①②④
    （填上你认为正确的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    任何一个正整数n都可以进行这样的分解： （s、t是正整数，且s≤t），如果在n的所有这种分解中两因数之差的绝对值最小，我们就称（）是n的最佳分解，并规定．例如：18可以分解成1×18，2×9，3×6，这时就有．结合以上信息，给出下列关于的说法：①；②；③；④若n是一个整数的平方，则．其中正确的说法有_________.（只填序号）

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏盐城第一初级中学七年级上学期期中考试数学试卷（带解析） 题型：解答题

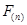    任何一个正整数n都可以进行这样的分解： （s、t是正整数，且s≤t），如果在n的所有这种分解中两因数之差的绝对值最小，我们就称（）是n的最佳分解，并规定．例如：18可以分解成1×18，2×9，3×6，这时就有．结合以上信息，给出下列关于的说法：①；②；③；④若n是一个整数的平方，则．其中正确的说法有_________.（只填序号）

    查看答案和解析>>

    同步练习册答案