
分析 原式括号中利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,由已知方程求出x的值,代入计算即可求出值.
解答 解:原式=$\frac{x-2}{x-1}$÷$\frac{(x+2)(x-2)}{x-1}$=$\frac{x-2}{x-1}$•$\frac{x-1}{(x+2)(x-2)}$=$\frac{1}{x+2}$,
由x2-2x-8=0,变形得:(x-4)(x+2)=0,
解得:x=4或x=-2,
当x=-2时,原式没有意义,舍去;
当x=4时,原式=$\frac{1}{6}$.
点评 此题考查了分式的化简求值,以及一元二次方程的解法,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 12个 | B. | 16个 | C. | 20个 | D. | 30个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
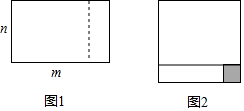 如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )
如图1,把一个长为m、宽为n的长方形(m>n),沿虚线剪开,将其与阴影部分所表示的小正方形一起拼接成如图2所示的长方形,则下列说法不正确的是( )| A. | 图2所示的长方形是正方形 | |
| B. | 图2所示的长方形周长=2m+2n | |
| C. | 阴影部分所表示的小正方形边长=m-n | |
| D. | 阴影部分所表示的小正方形面积=$\frac{(m-n)^{2}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是4$\sqrt{5}$.
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是4$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
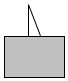 如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )
如图中的三角形被木板遮住了一部分,被遮住的两个角不可能是( )| A. | 一个锐角 一个钝角 | B. | 两个锐角 | ||
| C. | 一个锐角 一个直角 | D. | 一个直角 一个钝角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小明家小区空地上有两棵笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=32°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点.在一条直线上,求树EF的高度.(结果精确到0.1米,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.)
如图所示,小明家小区空地上有两棵笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=32°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A、B、C、E四点.在一条直线上,求树EF的高度.(结果精确到0.1米,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com