
°æƒø°ø2018ƒÍ1‘¬19»’£¨÷–≈∑£®œ√√≈-Œ˜∞≤-≤º¥Ô≈ÂÀπ£©∞ý¡– ª≥ˆœ√√≈◊‘√≥«¯∫£≤◊ª≥µ’棨æ≠Œ˜∞≤÷±¥Ô–Ÿ—¿¿˚ ◊∂º≤º¥Ô≈ÂÀ𠣨Œ“ –”Î≈∑÷Þ∏˜π˙æ≠√≥Õ˘¿¥»’“Ê∆µ∑±£¨ƒ≥≈∑÷ÞøÕ…Ã◊º±∏‘⁄œ√√≈≤…π∫“ª≈˙Ãÿ…´…Ã∆∑£¨æ≠µ˜≤È£¨”√![]() ‘™≤…π∫
‘™≤…π∫![]() –Õ…Ã∆∑µƒº˛ ˝ «”√
–Õ…Ã∆∑µƒº˛ ˝ «”√![]() ‘™≤…π∫
‘™≤…π∫![]() –Õ…Ã∆∑º˛ ˝µƒ
–Õ…Ã∆∑º˛ ˝µƒ![]() ±∂£¨“ªº˛
±∂£¨“ªº˛![]() –Õ…Ã∆∑µƒΩ¯º€±»“ªº˛
–Õ…Ã∆∑µƒΩ¯º€±»“ªº˛![]() –Õ…Ã∆∑µƒΩ¯º€∂ý
–Õ…Ã∆∑µƒΩ¯º€∂ý![]() ‘™.
‘™.
£®1£©«Û“ªº˛![]() –Õ…Ã∆∑µƒΩ¯º€∑÷±Œ™∂ý…Ÿ‘™£ø
–Õ…Ã∆∑µƒΩ¯º€∑÷±Œ™∂ý…Ÿ‘™£ø
£®2£©»Ù∏√≈∑÷ÞøÕ…Ãπ∫Ω¯![]() –Õ…Ã∆∑π≤
–Õ…Ã∆∑π≤![]() º˛Ω¯–– ‘œ˙£¨∆‰÷–
º˛Ω¯–– ‘œ˙£¨∆‰÷–![]() –Õ…Ã∆∑µƒº˛ ˝≤ª¥Û”⁄
–Õ…Ã∆∑µƒº˛ ˝≤ª¥Û”⁄![]() –Õ…Ã∆∑µƒº˛ ˝£¨«“≤ª–°”⁄
–Õ…Ã∆∑µƒº˛ ˝£¨«“≤ª–°”⁄![]() º˛£¨“—÷™
º˛£¨“—÷™![]() –Õ…Ã∆∑µƒ €º€Œ™
–Õ…Ã∆∑µƒ €º€Œ™![]() ‘™/º˛£¨
‘™/º˛£¨![]() –Õ…Ã∆∑µƒ €º€Œ™
–Õ…Ã∆∑µƒ €º€Œ™![]() ‘™/º˛£¨«“»´≤ø €≥ˆ£¨…Ëπ∫Ω¯
‘™/º˛£¨«“»´≤ø €≥ˆ£¨…Ëπ∫Ω¯![]() –Õ…Ã∆∑
–Õ…Ã∆∑![]() º˛.
º˛.
¢Ÿ«Û∏√øÕ…Ãœ˙ €’‚≈˙…Ã∆∑µƒ¿˚»Û![]() ”Î
”Î![]() ÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£ª
÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£ª
¢⁄»Ù≈∑÷Þ…Ãæˆ∂®‘⁄ ‘œ˙ªÓ∂Ø÷–√ø €≥ˆ“ªº˛![]() –Õ…Ã∆∑£¨æÕ¥”“ªº˛
–Õ…Ã∆∑£¨æÕ¥”“ªº˛![]() –Õ…Ã∆∑µƒ¿˚»Û÷–æËœ◊¥»…∆◊ Ω
–Õ…Ã∆∑µƒ¿˚»Û÷–æËœ◊¥»…∆◊ Ω![]() ‘™£¨«Û∏√øÕ…Ã €ÕÍÀ˘”–…Ã∆∑≤¢æËœ◊◊ Ω∫ÛªÒµ√µƒ◊Ó¥Û ’“Ê.
‘™£¨«Û∏√øÕ…Ã €ÕÍÀ˘”–…Ã∆∑≤¢æËœ◊◊ Ω∫ÛªÒµ√µƒ◊Ó¥Û ’“Ê.
°æ¥∞∏°ø£®1£©![]() –Õ…Ã∆∑µƒΩ¯º€
–Õ…Ã∆∑µƒΩ¯º€![]() ‘™£¨
‘™£¨![]() …Ã∆∑µƒΩ¯º€Œ™
…Ã∆∑µƒΩ¯º€Œ™![]() ‘™£ª
‘™£ª
£®2£©¢Ÿ![]() £ª
£ª
¢⁄µ±![]() ±£¨
±£¨![]() ±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®
±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®![]() £©‘™£ª
£©‘™£ª
µ±![]() ±£¨◊Ó¥Û¿˚“ÊŒ™£∫17500‘™£ª
±£¨◊Ó¥Û¿˚“ÊŒ™£∫17500‘™£ª
µ±![]() ±£¨
±£¨![]() ±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®
±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®![]() £©‘™.
£©‘™.
°æΩ‚Œˆ°ø
£®1£©£©…Ë“ªº˛![]() –Õ…Ã∆∑µƒΩ¯º€Œ™
–Õ…Ã∆∑µƒΩ¯º€Œ™![]() ‘™£¨‘Ú
‘™£¨‘Ú![]() –Õ…Ã∆∑µƒΩ¯º€Œ™
–Õ…Ã∆∑µƒΩ¯º€Œ™![]() ‘™£¨∏˘æð”√
‘™£¨∏˘æð”√![]() ‘™≤…π∫
‘™≤…π∫![]() –Õ…Ã∆∑µƒº˛ ˝ «”√
–Õ…Ã∆∑µƒº˛ ˝ «”√![]() ‘™≤…π∫
‘™≤…π∫![]() –Õ…Ã∆∑º˛ ˝µƒ
–Õ…Ã∆∑º˛ ˝µƒ![]() ±∂£¨¡–≥ˆ∑Ω≥ú¥ø…«ÛΩ‚£ª
±∂£¨¡–≥ˆ∑Ω≥ú¥ø…«ÛΩ‚£ª
£®2£©¢Ÿ∏˘æð◊п˚»Û=¡Ω÷÷…Ã∆∑µƒ¿˚»Û÷Æ∫Õ£¨¡–≥ˆ Ω◊”º¥ø…Ω‚æˆŒ £ª
¢⁄…ËæËœ◊◊ Ω∫ÛªÒ¿˚Œ™![]() ‘™£¨‘Ú
‘™£¨‘Ú![]() £¨∑÷»˝÷÷«È–ŒÃ÷¬€º¥ø…Ω‚æˆŒ £Æ
£¨∑÷»˝÷÷«È–ŒÃ÷¬€º¥ø…Ω‚æˆŒ £Æ
Ω‚£∫£®1£©…Ë“ªº˛![]() –Õ…Ã∆∑µƒΩ¯º€Œ™
–Õ…Ã∆∑µƒΩ¯º€Œ™![]() ‘™£¨‘Ú
‘™£¨‘Ú![]() –Õ…Ã∆∑µƒΩ¯º€Œ™
–Õ…Ã∆∑µƒΩ¯º€Œ™![]() ‘™£¨
‘™£¨
![]() £¨
£¨
Ω‚µ√![]() £¨
£¨
æ≠ºÏ—È![]() «‘≠∑Ω≥õƒΩ‚£¨«“∑˚∫œÃ‚“‚£¨
«‘≠∑Ω≥õƒΩ‚£¨«“∑˚∫œÃ‚“‚£¨
![]() …Ã∆∑µƒΩ¯º€Œ™‘™
…Ã∆∑µƒΩ¯º€Œ™‘™![]() £¨
£¨
¥£∫![]() –Õ…Ã∆∑µƒΩ¯º€
–Õ…Ã∆∑µƒΩ¯º€![]() ‘™£¨
‘™£¨![]() …Ã∆∑µƒΩ¯º€Œ™
…Ã∆∑µƒΩ¯º€Œ™![]() ‘™£ª
‘™£ª
£®2£©¢Ÿ…Ë![]() –Õ…Ã∆∑
–Õ…Ã∆∑![]() º˛£¨‘Ú
º˛£¨‘Ú![]() –Õ…Ã∆∑
–Õ…Ã∆∑![]() º˛£¨‘Ú
º˛£¨‘Ú
![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
¢⁄…ËæËœ◊◊ Ω∫ÛªÒ¿˚Œ™![]() ‘™£¨
‘™£¨
![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() ÀÊ
ÀÊ![]() µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨
µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨
![]() µ±
µ±![]() ±¿˚»Û◊Ó¥Û£¨
±¿˚»Û◊Ó¥Û£¨![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() £¨
£¨
µ±![]() ±
±![]() ÀÊ
ÀÊ![]() µƒ‘ˆ¥Û∂¯ºı–°£¨
µƒ‘ˆ¥Û∂¯ºı–°£¨
![]() µ±
µ±![]() ±£¨¿˚»Û◊Ó¥Û£¨
±£¨¿˚»Û◊Ó¥Û£¨![]() .
.
π ¥∞∏Œ™£∫£®1£©![]() –Õ…Ã∆∑µƒΩ¯º€
–Õ…Ã∆∑µƒΩ¯º€![]() ‘™£¨
‘™£¨![]() …Ã∆∑µƒΩ¯º€Œ™
…Ã∆∑µƒΩ¯º€Œ™![]() ‘™£ª
‘™£ª
£®2£©¢Ÿ![]() £ª
£ª
¢⁄µ±![]() ±£¨
±£¨![]() ±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®
±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®![]() £©‘™£ª
£©‘™£ª
µ±![]() ±£¨◊Ó¥Û¿˚“ÊŒ™£∫17500‘™£ª
±£¨◊Ó¥Û¿˚“ÊŒ™£∫17500‘™£ª
µ±![]() ±£¨
±£¨![]() ±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®
±¿˚»Û◊Ó¥Û£¨◊Ó¥Û¿˚“ÊŒ™£∫£®![]() £©‘™.
£©‘™.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() µƒ∂•µ„Œ™
µƒ∂•µ„Œ™![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() £¨
£¨![]() ¡Ωµ„£®µ„
¡Ωµ„£®µ„![]() ‘⁄µ„
‘⁄µ„![]() µƒ◊Û≤ý£©°£
µƒ◊Û≤ý£©°£
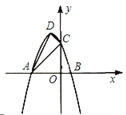
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©¡¨Ω”![]() £¨
£¨![]() £¨
£¨![]() £¨ ‘÷§√˜
£¨ ‘÷§√˜![]() Œ™÷±Ω«»˝Ω«–Œ£ª
Œ™÷±Ω«»˝Ω«–Œ£ª
£®3£©»Ùµ„![]() ‘⁄≈◊ŒÔœþ…œ£¨
‘⁄≈◊ŒÔœþ…œ£¨![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨“‘
£¨“‘![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒ»˝Ω«–Œ”Î
Œ™∂•µ„µƒ»˝Ω«–Œ”Î![]() œýÀ∆£¨ ‘«Û≥ˆÀ˘”–¬˙◊„Ãıº˛µƒµ„
œýÀ∆£¨ ‘«Û≥ˆÀ˘”–¬˙◊„Ãıº˛µƒµ„![]() µƒ◊¯±Í°£
µƒ◊¯±Í°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™µ„A£®4£¨0£©£¨OŒ™◊¯±Í‘≠µ„£¨P «œþ∂ŒOA…œ»Œ“‚“ªµ„£®≤ª∫¨∂Àµ„O£¨A£©£¨π˝P°¢O¡Ωµ„µƒ∂˛¥Œ∫Ø ˝y1∫Õπ˝P°¢A¡Ωµ„µƒ∂˛¥Œ∫Ø ˝y2µƒÕºœÛø™ø⁄æ˘œÚœ¬£¨À¸√«µƒ∂•µ„∑÷±Œ™B°¢C£¨…‰œþOB”ÎACœýΩª”⁄µ„D£Æµ±OD=AD=3 ±£¨’‚¡Ω∏ˆ∂˛¥Œ∫Ø ˝µƒ◊Ó¥Û÷µ÷Æ∫Õµ»”⁄£® £©

A£Æ![]() B£Æ
B£Æ![]() C£Æ3 D£Æ4
C£Æ3 D£Æ4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–”–“ª÷±Ω«»˝Ω«–ŒAOB£¨OŒ™◊¯±Í‘≠µ„£¨OA£Ω1£¨tan°œBAO£Ω3£¨Ω´¥À»˝Ω«–Œ»∆‘≠µ„OƒÊ ±’Ζ˝◊™90°„£¨µ√µΩ°˜DOC£¨≈◊ŒÔœþy£Ωax2+bx+cæ≠π˝µ„A°¢B°¢C£Æ
(1)«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
(2)»Ùµ„P «µ⁄∂˛œÛœÞƒ⁄≈◊ŒÔœþ…œµƒ∂ص„£¨∆‰∫·◊¯±ÍŒ™t£¨…Ë≈◊ŒÔœþ∂‘≥∆÷·l”Îx÷·Ωª”⁄“ªµ„E£¨¡¨Ω”PE£¨ΩªCD”⁄F£¨«Û“‘C°¢E°¢FŒ™∂•µ„»˝Ω«–Œ”ΰ˜CODœýÀ∆ ±µ„Pµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
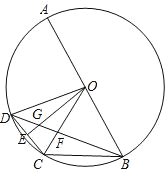
°æƒø°ø»ÁÕº£¨AB «°—Oµƒ÷±æ∂£¨œ“BC£ΩOB£¨µ„D «![]() …œ“ª∂ص„£¨µ„E «CD÷–µ„£¨¡¨Ω”BD∑÷±ΩªOC£¨OE”⁄µ„F£¨G£Æ
…œ“ª∂ص„£¨µ„E «CD÷–µ„£¨¡¨Ω”BD∑÷±ΩªOC£¨OE”⁄µ„F£¨G£Æ
(1)«Û°œDGEµƒ∂» ˝£ª
(2)»Ù![]() £Ω
£Ω![]() £¨«Û
£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
(3)º«°˜CFB£¨°˜DGOµƒ√ʪ˝∑÷±Œ™S1£¨S2£¨»Ù![]() £Ωk£¨«Û
£Ωk£¨«Û![]() µƒ÷µ£Æ(”√∫¨kµƒ Ω◊”±Ì æ)
µƒ÷µ£Æ(”√∫¨kµƒ Ω◊”±Ì æ)
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
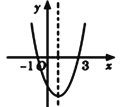
°æƒø°ø»ÁÕºŒ™∂˛¥Œ∫Ø ˝![]() µƒÕºœÛ£¨œ¬¡–Àµ∑®’˝»∑µƒ”–____________.
µƒÕºœÛ£¨œ¬¡–Àµ∑®’˝»∑µƒ”–____________.
¢Ÿ![]() £ª¢⁄
£ª¢⁄![]() £ª¢€
£ª¢€![]()
¢Ðµ±![]() ±£¨yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£ª
±£¨yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£ª
¢ð∑Ω≥Ã![]() µƒ∏˘ «
µƒ∏˘ «![]() £¨
£¨![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨≈◊ŒÔœþy£Ωax2+bx©Å3£®a°Ÿ0£©”Îx÷·Ωª”⁄µ„A£®©Å1£¨0£©∫Õµ„B£¨«“OB£Ω3OA£¨”Îy÷·Ωª”⁄µ„C£¨¥À≈◊ŒÔœþ∂•µ„Œ™µ„D£Æ
£®1£©«Û≈◊ŒÔœþµƒ±Ì¥Ô Ωº∞µ„Dµƒ◊¯±Í£ª
£®2£©»Áπ˚µ„E «y÷·…œµƒ“ªµ„£®µ„E”ε„C≤ª÷ÿ∫œ£©£¨µ±BE°ÕDE ±£¨«Ûµ„Eµƒ◊¯±Í£ª
£®3£©»Áπ˚µ„F «≈◊ŒÔœþ…œµƒ“ªµ„£Æ«“°œFBD£Ω135°„£¨«Ûµ„Fµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
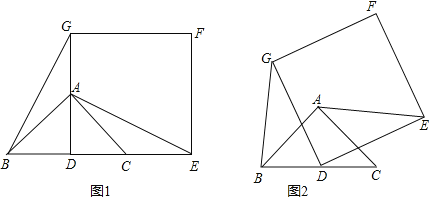
°æƒø°ø»ÁÕº1£¨“—÷™![]() «µ»—¸÷±Ω«»˝Ω«–Œ£¨
«µ»—¸÷±Ω«»˝Ω«–Œ£¨![]() £¨µ„D «BCµƒ÷–µ„
£¨µ„D «BCµƒ÷–µ„![]() ◊˜’˝∑Ω–ŒDEFG£¨ πµ„A°¢C∑÷±‘⁄DG∫ÕDE…œ£¨¡¨Ω”AE£¨BG£Æ
◊˜’˝∑Ω–ŒDEFG£¨ πµ„A°¢C∑÷±‘⁄DG∫ÕDE…œ£¨¡¨Ω”AE£¨BG£Æ
![]() ‘≤¬œÎœþ∂ŒBG∫ÕAEµƒ ˝¡øπÿœµ «______£ª
‘≤¬œÎœþ∂ŒBG∫ÕAEµƒ ˝¡øπÿœµ «______£ª
![]() Ω´’˝∑Ω–ŒDEFG»∆µ„DƒÊ ±’Î∑ΩœÚ–˝◊™
Ω´’˝∑Ω–ŒDEFG»∆µ„DƒÊ ±’Î∑ΩœÚ–˝◊™![]() £¨
£¨
![]() ≈–∂œ
≈–∂œ![]() ÷–µƒΩ·¬€ «∑Ò»‘»ª≥…¡¢£ø«Î¿˚”√Õº2÷§√˜ƒ„µƒΩ·¬€£ª
÷–µƒΩ·¬€ «∑Ò»‘»ª≥…¡¢£ø«Î¿˚”√Õº2÷§√˜ƒ„µƒΩ·¬€£ª
![]() »Ù
»Ù![]() £¨µ±AE»°◊Ó¥Û÷µ ±£¨«ÛAFµƒ÷µ£Æ
£¨µ±AE»°◊Ó¥Û÷µ ±£¨«ÛAFµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“‘…»–Œ OAB µƒ∂•µ„ O Œ™‘≠µ„£¨∞Îæ∂ OB À˘‘⁄µƒ÷±œþŒ™ x ÷·£¨Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ£¨µ„ B µƒ◊¯±ÍŒ™(2£¨0)£¨»Ù≈◊ŒÔœþ ![]() (n Œ™≥£ ˝)”Î…»–Œ OAB µƒ±þΩÁ◊Д–¡Ω∏ˆπ´π≤µ„‘Ú n µƒ»°÷µ∑∂Œß «( )
(n Œ™≥£ ˝)”Î…»–Œ OAB µƒ±þΩÁ◊Д–¡Ω∏ˆπ´π≤µ„‘Ú n µƒ»°÷µ∑∂Œß «( )

A.n>-4B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com