
【题目】如图,抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧)。
的左侧)。
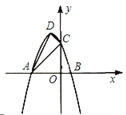
(1)求抛物线的解析式;
(2)连接![]() ,
,![]() ,
,![]() ,试证明
,试证明![]() 为直角三角形;
为直角三角形;
(3)若点![]() 在抛物线上,
在抛物线上,![]() 轴于点
轴于点![]() ,以
,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,试求出所有满足条件的点
相似,试求出所有满足条件的点![]() 的坐标。
的坐标。
【答案】(1)![]() ;(2)详见解析;(3)所有满足条件的点
;(2)详见解析;(3)所有满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]()
【解析】
(1)根据二次函数顶点坐标公式得到关于b,c的方程组,然后求解方程组即可;
(2)先求得A点坐标,再利用两点的距离公式求得△ACD的边长,然后根据勾股定理的逆定理即可得证;
(3)设![]() ,分两种情况讨论:①若
,分两种情况讨论:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ;分别代入求得符合题意的x的值即可得解.
;分别代入求得符合题意的x的值即可得解.
解:(1)由题意得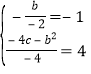 ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)令![]() ,解得
,解得![]() 或
或![]() ,
,
由题意点![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为直角三角形;
为直角三角形;
(3)设![]() ,分两种情况讨论:
,分两种情况讨论:
①若![]() ,如图1,
,如图1,
则![]() ,即
,即![]() ,
,
整理,得![]() ,
,
解得![]() ,
,![]() (与点
(与点![]() 重合,舍去),
重合,舍去),
当![]() 时,
时,![]() ,
,
∴此时,点![]() 的坐标为
的坐标为![]() ;
;
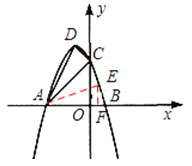
②若![]() ,如图2,
,如图2,
则![]() ,即
,即![]() ,
,
整理,得![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴此时,点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
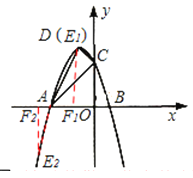
综上所述,所有满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
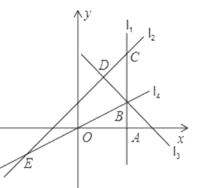
【题目】如图,直线 ![]() 轴于点
轴于点 ![]() ,点
,点![]() 是直线
是直线 ![]() 上的动点.直线
上的动点.直线 ![]() 交
交 ![]() 于点
于点 ![]() ,过点
,过点 ![]() 作直线
作直线 ![]() 垂直于
垂直于 ![]() ,垂足为
,垂足为 ![]() ,过点
,过点 ![]() ,
,![]() 的直线
的直线 ![]() 交
交 ![]() 于点 E,当直线
于点 E,当直线 ![]() ,
,![]() ,
,![]() 能围成三角形时,设该三角形面积为
能围成三角形时,设该三角形面积为 ![]() ,当直线
,当直线 ![]() ,
,![]() ,
,![]() 能围成三角形时,设该三角形面积为
能围成三角形时,设该三角形面积为 ![]() .
.
(1)若点 ![]() 在线段
在线段 ![]() 上,且
上,且 ![]() ,则
,则 ![]() 点坐标为_________;
点坐标为_________;
(2)若点 ![]() 在直线
在直线![]() 上,且
上,且![]() ,则
,则![]() 的度数为_______.
的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE均为等腰直角三角形,连接BE,点F、G分别为AD、AC的中点,连接FG.在△ADE绕A旋转的过程中,当B、D、E三点共线时,AB=![]() ,AD=1,则线段FG的长为___.
,AD=1,则线段FG的长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
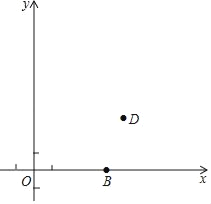
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 的图象经过点
的图象经过点![]() 、
、![]() ,设它与
,设它与![]() 轴的另一个交点为
轴的另一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() 的面积是3.
的面积是3.
(1)求该抛物线的表达式;
(2)求![]() 的正切值;
的正切值;
(3)若抛物线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 在射线
在射线![]() 上,当
上,当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
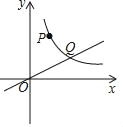
【题目】如图所示,直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (k≠0,x>0)的图象交于点Q(4,a),点P(m,n)是反比例函数图象上一点,且n=2m.
(k≠0,x>0)的图象交于点Q(4,a),点P(m,n)是反比例函数图象上一点,且n=2m.
(1)求点 P坐标;
(2)若点M在x轴上,使得△PMQ的面积为3,求M坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月19日,中欧(厦门-西安-布达佩斯)班列驶出厦门自贸区海沧火车站,经西安直达匈牙利首都布达佩斯 ,我市与欧洲各国经贸往来日益频繁,某欧洲客商准备在厦门采购一批特色商品,经调查,用![]() 元采购
元采购![]() 型商品的件数是用
型商品的件数是用![]() 元采购
元采购![]() 型商品件数的
型商品件数的![]() 倍,一件
倍,一件![]() 型商品的进价比一件
型商品的进价比一件![]() 型商品的进价多
型商品的进价多![]() 元.
元.
(1)求一件![]() 型商品的进价分别为多少元?
型商品的进价分别为多少元?
(2)若该欧洲客商购进![]() 型商品共
型商品共![]() 件进行试销,其中
件进行试销,其中![]() 型商品的件数不大于
型商品的件数不大于![]() 型商品的件数,且不小于
型商品的件数,且不小于![]() 件,已知
件,已知![]() 型商品的售价为
型商品的售价为![]() 元/件,
元/件,![]() 型商品的售价为
型商品的售价为![]() 元/件,且全部售出,设购进
元/件,且全部售出,设购进![]() 型商品
型商品![]() 件.
件.
①求该客商销售这批商品的利润![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
②若欧洲商决定在试销活动中每售出一件![]() 型商品,就从一件
型商品,就从一件![]() 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金![]() 元,求该客商售完所有商品并捐献资金后获得的最大收益.
元,求该客商售完所有商品并捐献资金后获得的最大收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com