【题目】如图，某消防队在一居民楼前进行演习，消防员利用云梯成功救出点B处的求救者后，又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°，点A距地面2.5米，点B距地面10.5米.为救出点C处的求救者，云梯需要继续上升的高度BC约为多少米？（结果保留整数.参考数据：tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,
≈1.4）
新编小学单元自测题系列答案科目：初中数学 来源： 题型：
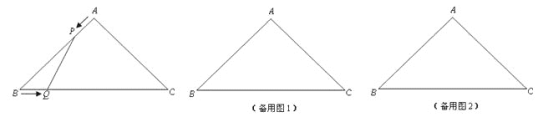
【题目】（1）如图1．在△ABC中，∠B=60°，∠DAC和∠ACE的角平分线交于点O，则∠O= °，
（2）如图2，若∠B=α，其他条件与（1）相同，请用含α的代数式表示∠O的大小；
（3）如图3，若∠B=α，
，则∠P= （用含α的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售，并分别以每箱35元与60元的价格出售，设购进A水果x箱，B水果y箱.
(1)让小王将水果全部售出共赚了215元，则小王共购进A、B水果各多少箱?
(2)若要求购进A水果的数量不得少于B水果的数量，则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润，此时最大利润是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC＝4cm，∠BAC＝90°．动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动．设点P的运动时间为ts，四边形APQC的面积为ycm2 ．
(1)当t为何值时，△PBQ是直角三角形?
(2)①求y与t的函数关系式，并写出t的取值范围；
②当t为何值时，y取得最小值？最小值为多少？
(3)设PQ的长为xcm，试求y与x的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
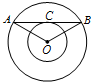
【题目】如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若∠AOB=120°，则大圆半径R与小圆半径r之间满足（ ）
A、
B、R=3r
C、R=2rD、
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】按要求完成下列视图问题
（1）如图（一），它是由
个同样大小的正方体摆成的几何体．将正方体①移走后，新几何体的三视图与原几何体的三视图相比，哪一个视图没有发生改变？
（2）如图（二），请你借助虚线网格（甲）画出该几何体的俯视图．
（3）如图（三），它是由几个小立方块组成的俯视图，小正方形上的数字表示该位置上的正方体的个数，请你借助虚线网格（乙）画出该几何体的主视图．
（4）如图（四），它是由
个大小相同的正方体组成的几何体的主视图和俯视图，请你借助虚线网格（丙）画出该几何体的左视图．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
