
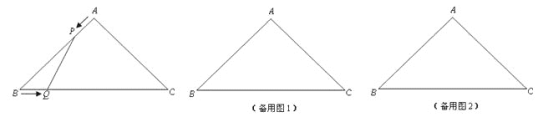
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃН4cmЃЌЁЯBACЃН90ЁуЃЎЖЏЕуPЁЂQЭЌЪБДгAЁЂBСНЕуГіЗЂЃЌЗжБ№биABЁЂBCЗНЯђдШЫйвЦЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧ1cm/sЃЌЕБЕуPЕНДяЕуBЪБЃЌPЁЂQСНЕуЭЃжЙдЫЖЏЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊtsЃЌЫФБпаЮAPQCЕФУцЛ§ЮЊycm2 ЃЎ
(1)ЕБtЮЊКЮжЕЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮ?
(2)ЂйЧѓyгыtЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіtЕФШЁжЕЗЖЮЇЃЛ
ЂкЕБtЮЊКЮжЕЪБЃЌyШЁЕУзюаЁжЕЃПзюаЁжЕЮЊЖрЩйЃП
(3)ЩшPQЕФГЄЮЊxcmЃЌЪдЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕБtЃН![]() Лђ
Лђ![]() ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЛЃЈ2ЃЉЂйyЃН8Ѓ
ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЛЃЈ2ЃЉЂйyЃН8Ѓ![]() ЃЈ0ЁмtЁм4ЃЉЃЌЂкЕБtЃН2ЪБЃЌyШЁЕУзюаЁжЕЃЌзюаЁжЕЪЧ
ЃЈ0ЁмtЁм4ЃЉЃЌЂкЕБtЃН2ЪБЃЌyШЁЕУзюаЁжЕЃЌзюаЁжЕЪЧ![]() ЃЛЃЈ3ЃЉy
ЃЛЃЈ3ЃЉy![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЗжЁЯPQBЃН90ЁуКЭЁЯQPBЃН90ЁуСНжжЧщПіЬжТлМДПЩЃЛ
ЃЈ2ЃЉИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНСаЪНyЃНSЁїABCЃSЁїBPQМДЕУКЏЪ§ЙиЯЕЪНЃЌИљОнЖўДЮКЏЪ§зюжЕдРэМДПЩЕУГіyШЁЕУзюаЁжЕЪБtЕФжЕКЭyЕФзюаЁжЕЃЛ
ЃЈ3ЃЉАбt2Ѓ4 tЃН![]() ДњШыyЃН8Ѓ
ДњШыyЃН8Ѓ![]() ЛЏМђМДПЩ.
ЛЏМђМДПЩ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЕБtЃН![]() Лђ
Лђ![]() ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЌРэгЩШчЯТЃК
ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮЃЌРэгЩШчЯТЃК
ЁпBQЃНAPЃНtЃЌ BPЃН4ЃtЃЌ
ЁрЂйЕБЁЯPQBЃН90ЁуЪБЃЌгЩ![]() ЕУЃК
ЕУЃК![]() t ЃН4ЃtЃЌНтЕУЃКtЃН
t ЃН4ЃtЃЌНтЕУЃКtЃН![]() ЃЛ
ЃЛ
ЂкЕБЁЯQPBЃН90ЁуЪБЃЌгЩ![]() ЕУЃК
ЕУЃК![]() ЃЌНтЕУЃКtЃН
ЃЌНтЕУЃКtЃН![]() .
.
ЁрЕБtЃН![]() Лђ
Лђ![]() ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮ.
ЪБЃЌЁїPBQЪЧжБНЧШ§НЧаЮ.
ЃЈ2ЃЉЂйЙ§PзїPHЁЭBCЃЌдкRtЁїPHBжаЃЌBPЃН4ЃtЃЌPHЃН![]() ЃЌ
ЃЌ
ЁрSЁїBPQЃН![]() ЃЌ
ЃЌ
ЁрyЃНSЁїABCЃSЁїBPQЃН8Ѓ![]() .
.
гЩЬтвтПЩжЊЃК0ЁмtЁм4.
ЂкyЃН8Ѓ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЕБtЃН2ЪБЃЌyШЁЕУзюаЁжЕЃЌзюаЁжЕЪЧ![]() ЃЎ
ЃЎ
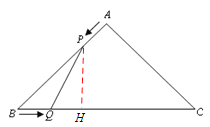
ЃЈ3ЃЉдкRtЁїPQHжаЃЌPHЃН![]() ЃЈ4ЃtЃЉЃЌHQЃН
ЃЈ4ЃtЃЉЃЌHQЃН![]() ЃЈ4ЃtЃЉЃtЃЌ
ЃЈ4ЃtЃЉЃtЃЌ
гЩPQ2ЃН PH2ЃЋHQ2ЃЌдђx2ЃНЁВ![]() ЃЈ4ЃtЃЉЁГ2ЃЋЁВ
ЃЈ4ЃtЃЉЁГ2ЃЋЁВ![]() ЃЈ4ЃtЃЉЃtЁГ2
ЃЈ4ЃtЃЉЃtЁГ2
ЛЏМђЕУЃКx2ЃНЃЈ2ЃЋ![]() ЃЉt 2Ѓ4ЃЈ2ЃЋ
ЃЉt 2Ѓ4ЃЈ2ЃЋ![]() ЃЉtЃЋ16ЃЌЁр t2Ѓ4 tЃН
ЃЉtЃЋ16ЃЌЁр t2Ѓ4 tЃН![]() .
.
НЋt2Ѓ4tЃН![]() ДњШыyЃН8Ѓ
ДњШыyЃН8Ѓ![]() ЃЌЕУyЃН8ЃЋ
ЃЌЕУyЃН8ЃЋ![]() ЁЄ
ЁЄ ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
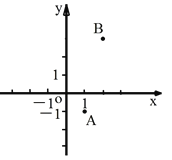
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЈ1ЃЌ-1ЃЉЃЌBЃЈ2ЃЌ3ЃЉЃЌЕуPЮЊxжсЩЯвЛЕуЃЌЕБ|PA-PB|ЕФжЕзюДѓЪБЃЌЕуPЕФзјБъЮЊЃЈЁЁЁЁЁЁЁЁ ЃЉ
A.ЃЈ-1ЃЌ0ЃЉB.ЃЈ![]() ЃЌ0ЃЉC.ЃЈ
ЃЌ0ЃЉC.ЃЈ![]() ЃЌ0ЃЉD.ЃЈ1ЃЌ0ЃЉ
ЃЌ0ЃЉD.ЃЈ1ЃЌ0ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBЃН45ЁуЃЌЁЯACBЃН60ЁуЃЌABЃН16ЃЌADЁЭBCЃЌДЙзуЮЊDЃЌЁЯACBЕФЦНЗжЯпНЛADгкЕуEЃЌдђAEЕФГЄЮЊЃЈЁЁЁЁЃЉ

A.![]() B.4
B.4![]() C.
C.![]()
![]() D.6
D.6![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєa+b=2ЃЌдђГЦaгыbЪЧЙигк1ЕФЦНКтЪ§ЃЎ
ЃЈ1ЃЉ3гыЁЁ ЁЁЪЧЙигк1ЕФЦНКтЪ§ЃЌ5Љ![]() гыЁЁ ЁЁЪЧЙигк1ЕФЦНКтЪ§ЃЛ
гыЁЁ ЁЁЪЧЙигк1ЕФЦНКтЪ§ЃЛ
ЃЈ2ЃЉШєЃЈm+![]() ЃЉЁСЃЈ1Љ
ЃЉЁСЃЈ1Љ![]() ЃЉ=Љ5+3
ЃЉ=Љ5+3![]() ЃЌХаЖЯm+
ЃЌХаЖЯm+![]() гы5Љ
гы5Љ![]() ЪЧЗёЪЧЙигк1ЕФЦНКтЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ЪЧЗёЪЧЙигк1ЕФЦНКтЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
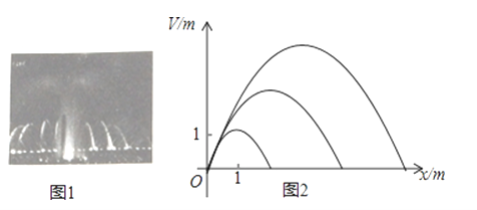
ЁОЬтФПЁПвєРжХчШЊЃЈЭМ1ЃЉПЩвдЪЙХчЫЎдьаЭЫцвєРжЕФНкзрЦ№ЗќБфЛЏЖјБфЛЏЃЎФГжжвєРжХчШЊаЮзДШчХзЮяЯпЃЌЩшЦфГіЫЎПкЮЊдЕуЃЌГіЫЎПкРыАЖБп18mЃЌвєРжБфЛЏЪБЃЌХзЮяЯпЕФЖЅЕудкжБЯпy=kxЩЯБфЖЏЃЌДгЖјВњЩњвЛзщВЛЭЌЕФХзЮяЯпЃЈЭМ2ЃЉЃЌетзщХзЮяЯпЕФЭГвЛаЮЪНЮЊy=ax2+bxЃЎ
ЃЈ1ЃЉШєвбжЊk=1ЃЌЧвХчГіЕФХзЮяЯпЫЎЯпзюДѓИпЖШДя3mЃЌЧѓДЫЪБaЁЂbЕФжЕЃЛ
ЃЈ2ЃЉШєk=1ЃЌХчГіЕФЫЎЧЁКУДяЕНАЖБпЃЌдђДЫЪБХчГіЕФХзЮяЯпЫЎЯпзюДѓИпЖШЪЧЖрЩйУзЃП
ЃЈ3ЃЉШєk=3ЃЌa=Љ![]() ЃЌдђХчГіЕФХзЮяЯпЫЎЯпФмЗёДяЕНАЖБпЃП
ЃЌдђХчГіЕФХзЮяЯпЫЎЯпФмЗёДяЕНАЖБпЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮжНЦЌABCDжаЃЌ ![]() ЃЌНЋСтаЮжНЦЌЗелЃЌЪЙЕуAТфдкCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕу
ЃЌНЋСтаЮжНЦЌЗелЃЌЪЙЕуAТфдкCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЩЯЃЌдђ
ЩЯЃЌдђ![]() ЕФжЕЮЊ______ ЃЎ
ЕФжЕЮЊ______ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГЯћЗРЖгдквЛОгУёТЅЧАНјаабнЯАЃЌЯћЗРдБРћгУдЦЬнГЩЙІОШГіЕуBДІЕФЧѓОШепКѓЃЌгжЗЂЯжЕуBе§ЩЯЗНЕуCДІЛЙгавЛУћЧѓОШеп.дкЯћЗРГЕЩЯЕуAДІВтЕУЕуBКЭЕуCЕФбіНЧЗжБ№ЪЧ45ЁуКЭ65ЁуЃЌЕуAОрЕиУц2.5УзЃЌЕуBОрЕиУц10.5Уз.ЮЊОШГіЕуCДІЕФЧѓОШепЃЌдЦЬнашвЊМЬајЩЯЩ§ЕФИпЖШBCдМЮЊЖрЩйУзЃПЃЈНсЙћБЃСєећЪ§.ВЮПМЪ§ОнЃКtan65ЁуЁж2.1,sin65ЁуЁж0.9,cos65ЁуЁж0.4,![]() Ёж1.4ЃЉ
Ёж1.4ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊABЮЊЁбOЕФжБОЖЃЌAB=2ЃЌADКЭBEЪЧдВOЕФСНЬѕЧаЯпЃЌAЁЂBЮЊЧаЕуЃЌЙ§дВЩЯвЛЕуCзїЁбOЕФЧаЯпCFЃЌЗжБ№НЛADЁЂBEгкЕуMЁЂNЃЌСЌНгACЁЂCBЃЌШєЁЯABC=30ЁуЃЌдђAM= ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
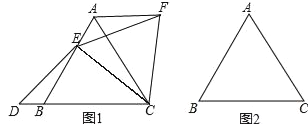
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЪЧЕШБпШ§НЧаЮЃЎ
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌЕуEдкЯпЖЮABЩЯЃЌЕуDдкЩфЯпCBЩЯЃЌЧвED=ECЃЎНЋЁїBCEШЦЕуCЫГЪБеыа§зЊ60ЁужСЁїACFЃЌСЌНгEFЃЎВТЯыЯпЖЮABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЃЛ
ЃЈ2ЃЉЕуEдкЯпЖЮBAЕФбгГЄЯпЩЯЃЌЦфЫќЬѕМўгыЃЈ1ЃЉжавЛжТЃЌЧыдкЭМЃЈ2ЃЉЕФЛљДЁЩЯНЋЭМаЮВЙГфЭъећЃЌВЂВТЯыЯпЖЮABЃЌDBЃЌAFжЎМфЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉЧыбЁдёЃЈ1ЃЉЛђЃЈ2ЃЉжаЕФвЛИіВТЯыНјаажЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com