
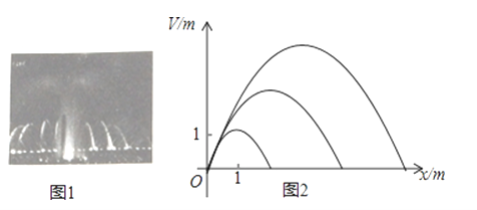
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
【答案】(1)a、b的值分别是![]() ,2;(2)喷出的抛物线水线最大高度是9米;(3)喷出的抛物线水线能达到岸边.
,2;(2)喷出的抛物线水线最大高度是9米;(3)喷出的抛物线水线能达到岸边.
【解析】
(1)根据抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,k=1,且喷出的抛物线水线最大高度达3m,可以求得a,b的值;
(2)根据k=1,喷出的水恰好达到岸边,抛物线的顶点在直线y=kx上,可以求得抛物线的对称轴x的值,从而可以得到此时喷出的抛物线水线最大高度;
(3)根据k=3,a=-![]() ,抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,可以求得b的值,然后令y=0代入抛物线的解析式,求得x的值,然后与18作比较即可解答本题.
,抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,可以求得b的值,然后令y=0代入抛物线的解析式,求得x的值,然后与18作比较即可解答本题.
(1)∵y=ax2+bx的顶点为(﹣![]() ),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
∴![]() ,
,![]() ,
,
解得,a=![]() ,b=2,
,b=2,
即k=1,且喷出的抛物线水线最大高度达3m,此时a、b的值分别是![]() ,2;
,2;
(2)∵k=1,喷出的水恰好达到岸边,出水口离岸边18m,抛物线的顶点在直线y=kx上,
∴此时抛物线的对称轴为x=9,y=x=9,
即此时喷出的抛物线水线最大高度是9米;
(3)∵y=ax2+bx的顶点为(﹣![]() )在直线y=3x上,a=﹣
)在直线y=3x上,a=﹣![]() ,
,
∴![]() ,
,
解得,b=6,
∴抛物线y=![]() ,
,
当y=0时,0=![]() ,
,
解得,x1=21,x2=0,
∵21>18,
∴若k=3,a=﹣![]() ,则喷出的抛物线水线能达到岸边,
,则喷出的抛物线水线能达到岸边,
即若k=3,a=﹣![]() ,喷出的抛物线水线能达到岸边.
,喷出的抛物线水线能达到岸边.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: ①a+b+c<0;②a–b+c<0;③b+2a<0;④abc>0,其中正确的是 (填写正确的序号)。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:在平面直角坐标系内,O为坐标原点,线段AB两端点在坐标轴上且点A(﹣4,0),点B(0,3),将AB向右平移4个单位长度至OC的位置
(1)直接写出点C的坐标 ;
(2)如图2,过点C作CD⊥x轴于点D,在x轴正半轴有一点E(1,0),过点E作x轴的垂线,在垂线上有一动点P,直接写出:①点D的坐标 ; ②三角形PCD的面积为 ;
(3)如图3,在(2)的条件下,连接AC,当△ACP的面积为![]() 时,直接写出点P的坐标 .
时,直接写出点P的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.
(1)让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?
(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
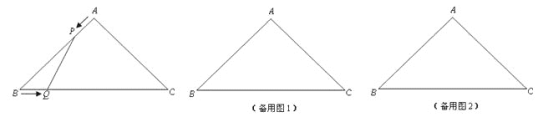
【题目】如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为ts,四边形APQC的面积为ycm2 .
(1)当t为何值时,△PBQ是直角三角形?
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com