
【题目】如图,已知△ABC是等边三角形.
(1)如图(1),点E在线段AB上,点D在射线CB上,且ED=EC.将△BCE绕点C顺时针旋转60°至△ACF,连接EF.猜想线段AB,DB,AF之间的数量关系;
(2)点E在线段BA的延长线上,其它条件与(1)中一致,请在图(2)的基础上将图形补充完整,并猜想线段AB,DB,AF之间的数量关系;
(3)请选择(1)或(2)中的一个猜想进行证明.
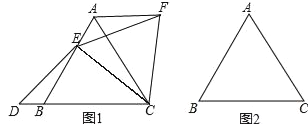
【答案】(1)猜想:AB=AF+BD;(2)猜想:AB=AF﹣BD;(3)AB=AF+BD.证明见解析.
【解析】整体分析:
(1)由于AF=BE,可能有BD=AE,因此猜想AB=AF+BD;(2)根据题意,画出图形,由图形猜想AB=AF﹣BD;(3)证猜想(1),过点E作EG∥BC交AC于点G,则△AEG为等边三角形,可证△BDE≌△GEC,得BD=AE,即可证明.
解:(1)猜想:AB=AF+BD;
(2)如图2,猜想:AB=AF﹣BD;
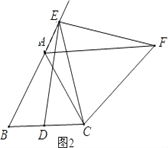
(3)如图(1),过点E作EG∥BC交AC于点G,得△AEG为等边三角形,

∵DE=CE,
∴∠CDE=∠ECD,
又∵∠CDE+∠BED=∠ABC=∠ACD=∠ECD+∠GCE,
∴∠BED=∠GCE,
在△BDE和△GEC中,
 ,
,
∴△BDE≌△GEC,
∴BD=EG=AE
又∵AF=BE,
∴AB=BE+AE=AF+BD.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为ts,四边形APQC的面积为ycm2 .
(1)当t为何值时,△PBQ是直角三角形?
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列视图问题

(1)如图(一),它是由![]() 个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助虚线网格(甲)画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助虚线网格(乙)画出该几何体的主视图.
(4)如图(四),它是由![]() 个大小相同的正方体组成的几何体的主视图和俯视图,请你借助虚线网格(丙)画出该几何体的左视图.
个大小相同的正方体组成的几何体的主视图和俯视图,请你借助虚线网格(丙)画出该几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“铁路建设助推经济发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了120千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加![]() m%小时,求m的值.
m%小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
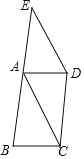
【题目】如图,已知四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接DE,AC
(1)求证:四边形ACDE为平行四边形;
(2)连接CE交AD于点O,若AC=AB=3,cosB=![]() ,求线段CE的长.
,求线段CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com