练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线与反比例函数的图像在第一象限有一个公共点，其横坐标为1，则一次函数的图像可能是（ ）

    A.

    B.

    C.

    D.

    【答案】B

    【解析】根据抛物线y=ax2+bx+c与反比例函数y=的图象在第一象限有一个公共点，可得b＞0，根据交点横坐标为1，可得a+b+c=b，可得a，c互为相反数，依此可得一次函数y=bx+ac的图象．

    解：∵抛物线y=ax2+bx+c与反比例函数y=的图象在第一象限有一个公共点，

    ∴b＞0，

    ∵交点横坐标为1，∴a+b+c=b，∴a+c=0，∴ac＜0，

    ∴一次函数y=bx+ac的图象经过第一、二、三象限．

    故选B．

    “点睛”考查了一次函数的图象，反比例函数的性质，二次函数的性质，关键是得到b＞0，ac＜0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB的垂直平分线EF交BC于点E，交AB于点F，D为线段CE的中点，BE=AC．

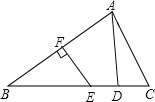
    （1）求证：AD⊥BC．

    （2）若∠BAC=75°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的方程

    （1）若这个方程有实数根，求实数k的取值范围；

    （2）若方程两实数根分别为x1、x2，且满足,求实数k的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】反比例函数y=的图象向右平移个单位长度得到一个新的函数，当自变量x取1，2，3，4，5，…，（正整数）时，新的函数值分别为y1，y2，y3，y4，y5，…，其中最小值和最大值分别为（　　）

    A. y1，y2 B. y43，y44 C. y44，y45 D. y2014，y2015

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】24.在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．

    （1）求证：四边形BFDE为平行四边形；

    （2）若四边形BFDE为菱形，且AB=2，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直线上摆放着三个正方形

    (1)如图1，已知水平放置的两个正方形的边长依次是，斜着放置的正方形的面积_ ；两个直角三角形的面积之和为____ (均用表示)

    (2)如图2，小正方形面积， 斜着放置的正方形的面积，求图中两个钝角三角形的面积_ ；_

    (3)图3是由五个正方形所搭成的平面图，与分别表示所在地三角形与正方形的面积，试写出_ ；_ .(均用表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知双曲线y＝(k＞0)的图象经过Rt△OAB的斜边OB的中点D，与直角边AB相交于点C.当BC＝OA＝6时，k＝___．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某网店销售单价分别为元/筒、元/筒的甲、乙两种羽毛球.根据消费者需求，该网店决定用不超过元购进甲、乙两种羽毛球共简.且甲种羽毛球的数量大于乙种羽毛球数量的.已知甲、乙两种羽毛球的进价分别为元/筒、元/筒。若设购进甲种羽毛球简.

    （1）该网店共有几种进货方案?

    （2）若所购进羽毛球均可全部售出，求该网店所获利润（元）与甲种羽毛球进货量（简）之间的函数关系式，并求利润的最大值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列方程的特征及其解的特点．

    ①x＋＝－3的解为x1＝－1，x2＝－2；

    ②x＋＝－5的解为x1＝－2，x2＝－3；

    ③x＋＝－7的解为x1＝－3，x2＝－4.

    解答下列问题：

    (1)请你写出一个符合上述特征的方程为________，其解为________；

    (2)根据这类方程的特征，写出第n个方程为________，其解为________；

    (3)请利用(2)的结论，求关于x的方程x＋＝－2(n＋2)(其中n为正整数)的解．

    查看答案和解析>>

    同步练习册答案