
【题目】如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
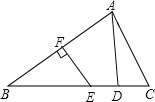
(1)求证:AD⊥BC.
(2)若∠BAC=75°,求∠B的度数.
【答案】(1)详见解析,(2)35°.
【解析】
(1)连接AE,根据垂直平分线的性质,可知BE=AE=AC,根据等腰三角形三线合一即可知AD⊥BC
(2)设∠B=x°,由(1)可知∠BAE=∠B=x°,然后根据三角形ABC的内角和为180°列出方程即可求出x的值.
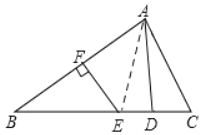
(1)连接AE,
∵EF垂直平分AB,
∴AE=BE,
∵BE=AC,
∴AE=AC,
∵D是EC的中点,
∴AD⊥BC;
(2)设∠B=x°,
∵AE=BE,
∴∠BAE=∠B=x°,
∴由三角形的外角的性质,∠AEC=2x°,
∵AE=AC,
∴∠C=∠AEC=2x°,
在三角形ABC中,3x°+75°=180°,
x°=35°,
∴∠B=35°.


科目:初中数学 来源: 题型:
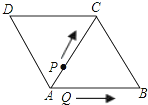
【题目】如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动。设P、Q运动的时间为t秒
(1)当t=2时,PQ=___;
(2)求点P、Q从出发到相遇所用的时间;
(3)当t取何值时,△APQ是等边三角形;请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
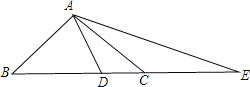
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强的钱包内有10元钱、20元钱和50元钱的纸币各1张.
(1)若从中随机取出1张纸币,求取出纸币的金额是20元的概率;
(2)若从中随机取出2张纸币,求取出纸币的总额可购买一件51元的商品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数![]() 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).
(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出ΔAPC≌ΔAPD的是( )

A.BC=BD B.∠ACB=∠ADB C.AC=AD D.∠CAB=∠DAB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com