
【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数![]() 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).
(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

【答案】(1)反比例函数的解析式为![]() ;一次函数的解析式为y=-x+1;(2)满足条件的P点的坐标为(-1+
;一次函数的解析式为y=-x+1;(2)满足条件的P点的坐标为(-1+![]() ,0)或(-1-
,0)或(-1-![]() ,0)或(2+
,0)或(2+![]() ,0)或(2-
,0)或(2-![]() ,0)或(0,0).
,0)或(0,0).
【解析】
(1)将A点代入求出k2,从而求出反比例函数方程,再联立将B点代入即可求出一次函数方程.
(2)令PA=PB,求出P.令AP=AB,求P.令BP=BA,求P.根据坐标距离公式计算即可.
(1)把A(-1,2)代入![]() ,得到k2=-2,
,得到k2=-2,
∴反比例函数的解析式为![]() .
.
∵B(m,-1)在![]() 上,∴m=2,
上,∴m=2,
由题意![]() ,解得:
,解得:![]() ,∴一次函数的解析式为y=-x+1.
,∴一次函数的解析式为y=-x+1.
(2)满足条件的P点的坐标为(-1+![]() ,0)或(-1-
,0)或(-1-![]() ,0)或(2+
,0)或(2+![]() ,0)或(2-
,0)或(2-![]() ,0)或(0,0).
,0)或(0,0).


科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间可供游客居住,当每个房间每天的定价为180元时,房间会全部住满,当每个房间每天的定价增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间的定价增加x元(x为10的整数倍),此时入住的房间数为y间,宾馆每天的利润为w元.
(1)直接写出y(间)与x(元)之间的函数关系;
(2)如何定价才能使宾馆每天的利润w(元)最大?
(3)若宾馆每天的利润为10800元,则每个房间每天的定价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
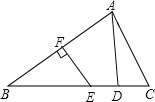
(1)求证:AD⊥BC.
(2)若∠BAC=75°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.
(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1 , 四边形DECB的面积为S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )
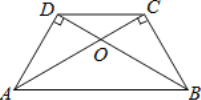
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(3)班共有学生54人,学习委员调查了班级学生参加课外活动的情况(每人只参加一项活动),其中:参加读书活动的18人,参加科技活动的人数占全班总人数的![]() ,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )
,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )
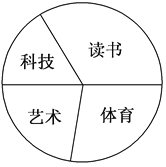
A. 100° B. 110°
C. 120° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF= ![]() ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com